题目内容
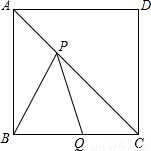
如图，在边长为2cm的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，连接PB、PQ，则△PBQ周长的最小值为分析：由于点B与点D关于AC对称，所以如果连接DQ，交AC于点P，那么△PBQ的周长最小，此时△PBQ的周长=BP+PQ+BQ=DQ+BQ．在Rt△CDQ中，由勾股定理先计算出DQ的长度，再得出结果．
解答：
解：连接DQ，交AC于点P，连接PB、BD，BD交AC于O．
∵四边形ABCD是正方形，
∴AC⊥BD，BO=OD，CD=2cm，
∴点B与点D关于AC对称，
∴BP=DP，
∴BP+PQ=DP+PQ=DQ．
在Rt△CDQ中，DQ=
=
=
cm，
∴△PBQ的周长的最小值为：BP+PQ+BQ=DQ+BQ=
+1（cm）．
故答案为：（
+1）．
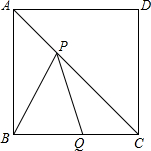
解：连接DQ，交AC于点P，连接PB、BD，BD交AC于O．∵四边形ABCD是正方形，
∴AC⊥BD，BO=OD，CD=2cm，
∴点B与点D关于AC对称，
∴BP=DP，
∴BP+PQ=DP+PQ=DQ．
在Rt△CDQ中，DQ=
| CD2+CQ2 |
| 22+12 |
| 5 |
∴△PBQ的周长的最小值为：BP+PQ+BQ=DQ+BQ=
| 5 |
故答案为：（
| 5 |
点评：根据两点之间线段最短，可确定点P的位置．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，问在E、F移动过程中：
，问在E、F移动过程中：
