题目内容

在边长为1的正方形网格中，正方形ABFE与正方形EFCD的位置如图所示．

（1）请你按下列要求画图：
①连接BD交EF于点M；
②在AE上取一点P，连接BP，MP，使△PEM与△PMB相似；
（2）若Q是线段BD上一点，连接FQ并延长交四边形ABCD的一边于点R，且满足 $数学公式$ ，则 $数学公式$ 的值为______．

解：（1）画图如图所示；

（2）如图，

当R在R₁的位置时， $\text{[math]}$ = $\text{[math]}$ =2，
当R在R₂的位置时， $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
当R在R₃的位置时， $\text{[math]}$ = $\text{[math]}$ =1．
故答案为：2， $\text{[math]}$ ，1．
分析：（1）根据题目的要求及网格的特点，作出图形即可；
（2）如图，根据题意，画出R点的三个可能的位置，分别计算 $\text{[math]}$ 的值．
点评：本题考查了相似三角形的判定与性质，正方形的性质．关键是能根据题意，利用相似三角形的判断画出图形，利用相似三角形的性质求解．

练习册系列答案

浙大优学中考探究题精析精练系列答案

励耘第二卷三年中考优化卷系列答案

中考必备中考真题精编系列答案

四川高考一轮复习导学案系列答案

经纶学典默写达人系列答案

名师讲坛1课1练系列答案

名师导航同步练与测系列答案

课堂感悟系列答案

经纶学典中考分类精华集系列答案

启东系列江苏省13大市中考真题汇编系列答案

相关题目

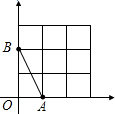如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．
（1）求线段AB所在直线的函数解析式，并写出当0≤y≤2时，自变量x的取值范围；
（2）将线段AB绕点B逆时针旋转90°，得到线段BC，请在答题卡指定位置画出线段BC．若直线BC的函数解析式为y=kx+b，则y随x的增大而

（填“增大”或“减小”）．

如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．
（1）若点P在图中所给网格中的格点上，△APB是等腰三角形，满足条件的点P共有

个．
（2）将线段AB沿x轴向右平移2格得线段CD，请你求出线段CD所在的直线函数解析式．

如图所示，在平面直角坐标系中，A、B、C、D均在边长为1的正方形网格格点上．
（1）求线段AB所在直线的解析式，并写出当0≤y≤2时，自变量x的取值范围；
（2）若把直线y=kx+b中的k叫做直线的斜率，那么直线AB和直线AD的斜率有什么关系？直线AB和直线CD的斜率有什么关系？

如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．

1.求线段AB所在直线的函数关系式，并写出当0≤y≤2时，自变量x的取值范围；

2.将线段AB绕点B逆时针旋转90°，得到线段BC，若直线BC的函数关系式为y=kx+b，则y随x的增大而（填“增大”或“减小”）．

如图8,在平面直角坐标系中,、均在边长为1的正方形网格格点上.

(1)求线段所在直线的函数解析式,并写出当时,自变量的取值范围；

(2)将线段绕点逆时针旋转,得到线段,请在指定位置画出线段.若直线的函数解析式为,则随的增大而 (填“增大”或“减小”).