题目内容
已知:△ABC中,∠ACB=2∠ABC,AD为∠BAC的平分线,E为线段AC上一点,过E作AD的垂线交直线AB于F.
(1)当E点与C点重合时(如图1),求证:BF=DE;
(2)连接BE交AD于点N,M是BF的中点,连接DM(如图2),若DM⊥BF,DC=4,S△ABD:S△ACD=3:2,求DN的长.
【答案】分析:(1)首先利用等角对等边即可证得AF=AE,则可以证明△AFD≌△AED,得到DF=DE,∠AFD=∠AED,根据则∠FBD=∠FDB,根据等角对等边可以证得;、
(2)根据三角形的面积公式即可得到BD:DC=3:2,即可求得BD和AB的长度,然后根据角平分线的性质,以及三角形的面积公式得到AB:AC=3:2,然后根据(1)的结论可以得到AQ=AM,DC=BM,则 =
= ,求得AC、AB的长度,然后根据勾股定理,列方程即可求得PC的长,则根据勾股定理求得AD的长度,然后证明△DAE∽△DEN,根据相似三角形的对应边的比相等,即可求解.
,求得AC、AB的长度,然后根据勾股定理,列方程即可求得PC的长,则根据勾股定理求得AD的长度,然后证明△DAE∽△DEN,根据相似三角形的对应边的比相等,即可求解.
解答: 证明:(1)连接DF,设AD与EF交于点K,
证明:(1)连接DF,设AD与EF交于点K,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵EF⊥AD,
∴∠AKF=∠AKE=90°,
∴∠AFK=∠AEK,
∴AF=AE,
则在△AFD和△AED中:
 ,
,
∴△AFD≌△AED,
∴DF=DE,∠AFD=∠AED,
又∵∠ACB=2∠ABC,
∴∠FBD=∠FDB,
∴BF=DF,
∴DE=BF;
(2)过A作AP⊥BC于点P,过D作DQ⊥AC于点Q.连接DF,
∵S△ABD:S△ACD=3:2,即 =
= ,
,
∴ =
= ,
,
∵DC=4,
∴BD=6
∵AD是∠BAC的平分线,DM⊥AB,DQ⊥AC,
∴DM=DQ,
∴ =
= ,
,
∴ =
= ,由(1)可得:AQ=AM,DC=BM,
,由(1)可得:AQ=AM,DC=BM,
∴AB=AC+DC,
∴ =
= ,
,
∴AC=8,AB=12,
设PC=x,则BP=10-x,又勾股定理得:AB2-BP2=AC2-PC2=AP2,
即122-(10-x)2=82-x2,解得:x=1,
∴DP=3,
又AD2-DP2=AC2-PC2=AP2,
∴AD2=72,AD=6 ,
,
∵EF⊥AD,
∴∠AKF=∠AKE=90°.
∵DA平分∠BAC,
∴∠FAD=∠EAD,
∴∠AFE=∠AEF
∴AF=AE
在△AFD和△AED中:

∴△AFD≌△AED,
∴∠AFD=∠AED,DF=DE,
又∵DB=DF,
∴DB=DE=6,
∴∠BFD=∠DEC=∠DBF,
∴180°-∠C-∠DEC=180°-∠C-∠DBF,
∴∠EDC=∠BAC=2∠DAE,
又∵∠EDC=2∠NED,
∴∠DAE=∠NED,
∵∠ADE=∠EDN,
∴△DAE∽△DEN,
∴ =
= ,
,
∴DE2=DN•DA,即62=DN•6 ,
,
∴DN=3 .
.
点评:本题考查了勾股定理,以及全等三角形的判定与性质,相似三角形的判定与性质,正确证明△DAE∽△DEN是关键.
(2)根据三角形的面积公式即可得到BD:DC=3:2,即可求得BD和AB的长度,然后根据角平分线的性质,以及三角形的面积公式得到AB:AC=3:2,然后根据(1)的结论可以得到AQ=AM,DC=BM,则
 =
= ,求得AC、AB的长度,然后根据勾股定理,列方程即可求得PC的长,则根据勾股定理求得AD的长度,然后证明△DAE∽△DEN,根据相似三角形的对应边的比相等,即可求解.
,求得AC、AB的长度,然后根据勾股定理,列方程即可求得PC的长,则根据勾股定理求得AD的长度,然后证明△DAE∽△DEN,根据相似三角形的对应边的比相等,即可求解.解答:
 证明:(1)连接DF,设AD与EF交于点K,
证明:(1)连接DF,设AD与EF交于点K,∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵EF⊥AD,
∴∠AKF=∠AKE=90°,
∴∠AFK=∠AEK,
∴AF=AE,
则在△AFD和△AED中:
 ,
,∴△AFD≌△AED,
∴DF=DE,∠AFD=∠AED,
又∵∠ACB=2∠ABC,
∴∠FBD=∠FDB,
∴BF=DF,
∴DE=BF;
(2)过A作AP⊥BC于点P,过D作DQ⊥AC于点Q.连接DF,
∵S△ABD:S△ACD=3:2,即
 =
= ,
,∴
 =
= ,
,∵DC=4,
∴BD=6
∵AD是∠BAC的平分线,DM⊥AB,DQ⊥AC,
∴DM=DQ,
∴
 =
= ,
,∴
 =
= ,由(1)可得:AQ=AM,DC=BM,
,由(1)可得:AQ=AM,DC=BM,∴AB=AC+DC,
∴
 =
= ,
,∴AC=8,AB=12,
设PC=x,则BP=10-x,又勾股定理得:AB2-BP2=AC2-PC2=AP2,
即122-(10-x)2=82-x2,解得:x=1,
∴DP=3,
又AD2-DP2=AC2-PC2=AP2,
∴AD2=72,AD=6
 ,
,∵EF⊥AD,
∴∠AKF=∠AKE=90°.
∵DA平分∠BAC,
∴∠FAD=∠EAD,
∴∠AFE=∠AEF
∴AF=AE
在△AFD和△AED中:

∴△AFD≌△AED,
∴∠AFD=∠AED,DF=DE,
又∵DB=DF,
∴DB=DE=6,
∴∠BFD=∠DEC=∠DBF,
∴180°-∠C-∠DEC=180°-∠C-∠DBF,
∴∠EDC=∠BAC=2∠DAE,
又∵∠EDC=2∠NED,
∴∠DAE=∠NED,
∵∠ADE=∠EDN,
∴△DAE∽△DEN,
∴
 =
= ,
,∴DE2=DN•DA,即62=DN•6
 ,
,∴DN=3
 .
.点评:本题考查了勾股定理,以及全等三角形的判定与性质,相似三角形的判定与性质,正确证明△DAE∽△DEN是关键.

练习册系列答案
相关题目
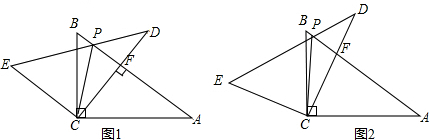
 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示) 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.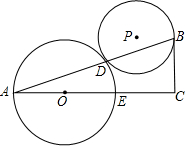 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,