题目内容
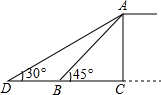 厦门市为缓解交通压力,决定修建人行天桥,原设计天桥的楼梯为AB,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°(如图所示).
厦门市为缓解交通压力,决定修建人行天桥,原设计天桥的楼梯为AB,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°(如图所示).(1)若原楼梯长AB=6米,求调整后楼梯AD的长;
(2)若BC=t米,求BD的长.(结果可以含t,保留根号)
分析:(1)首先由已知AB=6米,∠ABC=45°求出AC和BC,再根据∠ADC=30°,即可求得AD=2AC的值;
(2)根据BC=t,可知AC=t,然后在Rt△ADC中,根据∠D=30°,即可求出DC=
AC,继而可以求出BD.
(2)根据BC=t,可知AC=t,然后在Rt△ADC中,根据∠D=30°,即可求出DC=
| 3 |
解答:解:(1)在Rt△ABC中,
∵AB=6米,∠ABC=45°,
∴BC=AB•cos45°=3
,
∴AC=BC=3
,
在Rt△ADC中,∵∠D=30°,AC=3
,
∴AD=2AC=6
;
(2)在Rt△ABC中,∵BC=t,∠ABC=45°,
∴AC=t,
在Rt△ADC中,∵∠D=30°,AC=t,
∴DC=
=
t,
则BD=CD-BC=(
-1)t.
∵AB=6米,∠ABC=45°,
∴BC=AB•cos45°=3
| 2 |
∴AC=BC=3
| 2 |
在Rt△ADC中,∵∠D=30°,AC=3
| 2 |
∴AD=2AC=6
| 2 |
(2)在Rt△ABC中,∵BC=t,∠ABC=45°,
∴AC=t,
在Rt△ADC中,∵∠D=30°,AC=t,
∴DC=
| AC |
| tan30° |
| 3 |
则BD=CD-BC=(
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是掌握锐角三角函数的定义,能用已知线段及锐角三角函数值表示出未知线段.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
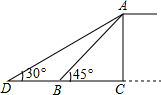 厦门市为缓解交通压力,决定修建人行天桥,原设计天桥的楼梯为AB,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°(如图所示).
厦门市为缓解交通压力,决定修建人行天桥,原设计天桥的楼梯为AB,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°(如图所示).