��Ŀ����
��ͼ��������y=��x2+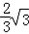 x+2��x�ύ��C��A���㣬��y�ύ�ڵ�B��OB=4����O����ֱ��AB�ĶԳƵ�ΪD��EΪ�߶�AB���е㣮
x+2��x�ύ��C��A���㣬��y�ύ�ڵ�B��OB=4����O����ֱ��AB�ĶԳƵ�ΪD��EΪ�߶�AB���е㣮
��1���ֱ������A����B�����ꣻ
��2����ֱ��AB�Ľ���ʽ��
��3��������������y= ��ͼ�����D����kֵ��
��ͼ�����D����kֵ��
��4��������P��Qͬʱ�ӵ�A�������ֱ���AB��AO������B��O�ƶ�����Pÿ���ƶ�1����λ����Qÿ���ƶ� ����λ�����POQ�����ΪS���ƶ�ʱ��Ϊt���ʣ�S�Ƿ�������ֵ�������ڣ����������ֵ���������ʱ��tֵ���������ڣ���˵�����ɣ�
����λ�����POQ�����ΪS���ƶ�ʱ��Ϊt���ʣ�S�Ƿ�������ֵ�������ڣ����������ֵ���������ʱ��tֵ���������ڣ���˵�����ɣ�
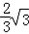 x+2��x�ύ��C��A���㣬��y�ύ�ڵ�B��OB=4����O����ֱ��AB�ĶԳƵ�ΪD��EΪ�߶�AB���е㣮
x+2��x�ύ��C��A���㣬��y�ύ�ڵ�B��OB=4����O����ֱ��AB�ĶԳƵ�ΪD��EΪ�߶�AB���е㣮��1���ֱ������A����B�����ꣻ
��2����ֱ��AB�Ľ���ʽ��
��3��������������y=
 ��ͼ�����D����kֵ��
��ͼ�����D����kֵ����4��������P��Qͬʱ�ӵ�A�������ֱ���AB��AO������B��O�ƶ�����Pÿ���ƶ�1����λ����Qÿ���ƶ�
 ����λ�����POQ�����ΪS���ƶ�ʱ��Ϊt���ʣ�S�Ƿ�������ֵ�������ڣ����������ֵ���������ʱ��tֵ���������ڣ���˵�����ɣ�
����λ�����POQ�����ΪS���ƶ�ʱ��Ϊt���ʣ�S�Ƿ�������ֵ�������ڣ����������ֵ���������ʱ��tֵ���������ڣ���˵�����ɣ�
�⣺��1����y=0������x2+  x+2=0��
x+2=0��
��� x1=�� ��x2=2
��x2=2  ��
��
��C���� ��0����A��2
��0����A��2 ��0������x=0����y=2��
��0������x=0����y=2��
��B��0��2�������ϣ�A��2 ��0����B��0��2����
��0����B��0��2����
��2����AB����Ϊy=k1x+2��Ϊ��A��2 ��0����ֱ���ϣ�
��0����ֱ���ϣ�
��0=k12 +2
+2
��k1=��
��ֱ��AB�Ľ���ʽΪy=�� x+2��
x+2��
��3����A��2 ��0����B��0��2���ã�OA=2
��0����B��0��2���ã�OA=2 ��OB=2��AB=4����BAO=30�㣬��DOA=60�㣻 OD��O�����AB�Գ�
��OB=2��AB=4����BAO=30�㣬��DOA=60�㣻 OD��O�����AB�Գ�
��OD=OA=2
��D��ĺ�����Ϊ ��������Ϊ3����D��
��������Ϊ3����D��  ��3����
��3����
��Ϊy= ����D��
����D��
��3= ��
��
��k=3 ��
��
��4��AP=t��AQ= t��P��x��ľ��룺AP��sin30��=
t��P��x��ľ��룺AP��sin30��= t��OQ=OA��AQ=2
t��OQ=OA��AQ=2 ��
�� t��
t��
��S��OPQ= ����2
����2 ��
�� t����
t���� t=��
t=�� ��t��2 ��2
��t��2 ��2 +
+  ��
��
�����⣬ ��0��t��4
��0��t��4
�൱t=2 ʱ��S�����ֵΪ
ʱ��S�����ֵΪ ��
��
 x+2=0��
x+2=0����� x1=��
 ��x2=2
��x2=2  ��
�� ��C����
 ��0����A��2
��0����A��2 ��0������x=0����y=2��
��0������x=0����y=2�� ��B��0��2�������ϣ�A��2
 ��0����B��0��2����
��0����B��0��2������2����AB����Ϊy=k1x+2��Ϊ��A��2
 ��0����ֱ���ϣ�
��0����ֱ���ϣ� ��0=k12
 +2
+2 ��k1=��

��ֱ��AB�Ľ���ʽΪy=��
 x+2��
x+2����3����A��2
 ��0����B��0��2���ã�OA=2
��0����B��0��2���ã�OA=2 ��OB=2��AB=4����BAO=30�㣬��DOA=60�㣻 OD��O�����AB�Գ�
��OB=2��AB=4����BAO=30�㣬��DOA=60�㣻 OD��O�����AB�Գ� ��OD=OA=2

��D��ĺ�����Ϊ
 ��������Ϊ3����D��
��������Ϊ3����D��  ��3����
��3������Ϊy=
 ����D��
����D�� ��3=
 ��
����k=3
 ��
����4��AP=t��AQ=
 t��P��x��ľ��룺AP��sin30��=
t��P��x��ľ��룺AP��sin30��= t��OQ=OA��AQ=2
t��OQ=OA��AQ=2 ��
�� t��
t�� ��S��OPQ=
 ����2
����2 ��
�� t����
t���� t=��
t=�� ��t��2 ��2
��t��2 ��2 +
+  ��
�������⣬
 ��0��t��4
��0��t��4 �൱t=2
 ʱ��S�����ֵΪ
ʱ��S�����ֵΪ ��
�� 
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������
��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������| A��-1��x��3 | B��3��x��-1 | C��x��-1��x��3 | D��x��-1��x��3 |
 26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG|
26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG| ��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4����
��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4���� ��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ� ����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮
����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮