题目内容
等边三角形ABC的边长为6，将其放置在如图所示的平面直角坐标系中，其中BC边在x轴上，BC边的高OA在Y轴上．一只电子虫从A出发，先沿y轴到达G点，再沿GC到达C点，已知电子虫在Y轴上运动的速度是在GC上运动速度的2倍，若电子虫走完全程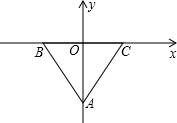
的时间最短，则点G的坐标为分析：先求出等边三角形BC边上的高为3
，设OG的长度为y，则AG的长度为3
-y，根据时间等于路程除以速度，设电子虫在y轴上的速度为2v，则在GC上的速度为v，列出时间表达式，再根据不等式当且仅当
=
时取最小值，求出y值，点G坐标可得．
| 3 |
| 3 |
3
| ||
| 2v |
| ||
| 2v |
解答：
解：根据题意，AO=6sin60°=3
，
如图，设OG长度为y，则AG=3
-y，
在Rt△OCG中，CG=
，
设电子虫在y轴上的速度为2v，则在GC上的速度为v，
所以电子虫走完全程的时间为t=
+
，
∵电子虫在Y轴上运动的速度是在GC上运动速度的2倍，
∴当且仅当
=
时，t有最小值，
即3
-y=2
，
整理得，y2-2
y+3=0，
解得y=
．
所以点G的坐标为（0，-
）．
故答案为：（0，-
）．
解：根据题意，AO=6sin60°=3| 3 |
如图，设OG长度为y，则AG=3
| 3 |
在Rt△OCG中，CG=
| y2+32 |
设电子虫在y轴上的速度为2v，则在GC上的速度为v，
所以电子虫走完全程的时间为t=
3
| ||
| 2v |
| ||
| v |
∵电子虫在Y轴上运动的速度是在GC上运动速度的2倍，
∴当且仅当
3
| ||
| 2v |
| ||
| 2v |
即3
| 3 |
| y2+32 |
整理得，y2-2
| 3 |
解得y=
| 3 |
所以点G的坐标为（0，-
| 3 |
故答案为：（0，-
| 3 |
点评：本题考查了等边三角形高的求法以及勾股定理的运用，利用不等式求最值是解题的关键．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
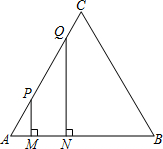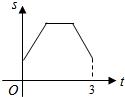
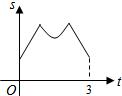
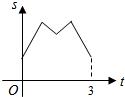
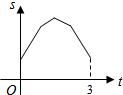
线段MN运动的时间为t秒．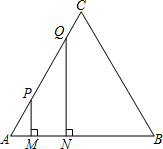
如图，等边三角形ABC的边长为4厘米，长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动（运动开始时，点M与点A重合，点N到达点B时运动终止），过点M、N分别作AB边的垂线，与△ABC的其它边交于P、Q两点．线段MN在运动的过程中，四边形MNQP的面积为S，运动的时间为t．则大致反映S与t变化关系的图象是（ ）
