Question

【题目】已知：点E、点G分别在直线AB、直线CD上，点F在两直线外，连接EF、FG

（1）如图1，AB∥CD，求证：∠AEF+∠FGC=∠EFG；

（2）若直线AB与直线CD不平行，连接EG，且EG同时平分∠BEF和∠FGD．

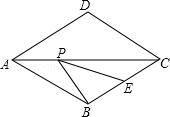
①如图2，请探究∠AEF、∠FGC、∠EFG之间的数量关系？并说明理由；

②如图3，∠AEF比∠FGC的3倍多10°，∠FGC是∠EFG的，则∠EFG=______°（直接写出答案）．

Answer 1

【答案】（1）证明见解析；（2）①2∠EFG=∠AEF+∠FGC；②25.

【解析】

（1）过F作FQ∥AB，利用平行线的性质，即可得到∠AEF+∠FGC=∠EFQ+∠GFQ=∠EFG；

（2）①延长AB，CD，交于点P，依据∠FEP=180°-∠AEF，∠FGP=180°-∠FGC，即可得到∠FEP+∠FGP=360°-（∠AEF+∠FGC），再根据四边形内角和，即可得到四边形EFGP中，∠F+∠P=360°-（∠FEP+∠FGP）=∠AEF+∠FGC，进而得出结论；

②根据2∠EFG=∠AEF+∠FGC，∠AEF比∠FGC的3倍多10°，∠FGC是∠EFG的，整理即可得到答案．

（1）如图1，过F作FQ∥AB，

∵AB∥CD，

∴PQ∥CD，

∴∠AEF=∠QFE，∠FGC=∠GFQ，

∴∠AEF+∠FGC=∠EFQ+∠GFQ=∠EFG；

（2）①如图2，延长AB，CD，交于点P，

∵EG同时平分∠BEF和∠FGD，

∴∠FEG=∠PEG，∠FGE=∠PGE，

∴∠F=∠P，

∵∠FEP=180°﹣∠AEF，∠FGP=180°﹣∠FGC，

∴∠FEP+∠FGP=360°﹣（∠AEF+∠FGC），

∵四边形EFGP中，∠F+∠P=360°﹣（∠FEP+∠FGP）=360°﹣[360°﹣（∠AEF+∠FGC）]=∠AEF+∠FGC，

即2∠EFG=∠AEF+∠FGC；

②由①可知：2∠EFG=∠AEF+∠FGC=3∠FGC+10°+∠FGC=4∠FGC+10°，

又∵∠FGC=∠EFG

∴2∠EFG=∠EFG+10°，

∴∠EFG=25°.

故答案为：25.