Question

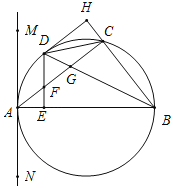
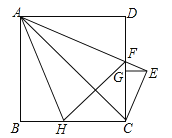
【题目】如图，边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH=DF，连接AH、FH，FH与AC交于点M，以下结论：

①FH=2BH；②AC⊥FH；③S△ACF=1；④CE=AF；⑤=FGDG，其中正确结论的个数为（　　）

A. 2 B. 3 C. 4 D. 5

Answer 1

【答案】C

【解析】①②如图1，∵四边形ABCD是正方形，∴AB=AD，∠B=∠D=90°，∠BAD=90°，∵AE平分∠DAC，∴∠FAD=∠CAF=22.5°，∵BH=DF，∴△ABH≌△ADF，∴AH=AF，∠BAH=FAD=22.5°，∴∠HAC=∠FAC，∴HM=FM，AC⊥FH，∵AE平分∠DAC，∴DF=FM，∴FH=2DF=2BH，故选项①②正确；

③在Rt△FMC中，∠FCM=45°，∴△FMC是等腰直角三角形，∵正方形的边长为2，∴AC=，MC=DF=﹣2，∴FC=2﹣DF=2﹣（﹣2）=4﹣，S△AFC=CFAD≠1，所以选项③不正确；

④AF===，∵△ADF∽△CEF，∴，∴，∴CE=，∴CE=AF，故选项④正确；

⑤在Rt△FEC中，EG⊥FC，∴=FGCG，cos∠FCE=，∴CG===1，∴DG=CG，∴=FGDG，故选项⑤正确；

本题正确的结论有4个，

故选C．