题目内容
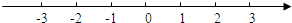 解下列方程组或不等式组:
解下列方程组或不等式组:
(1)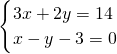
(2)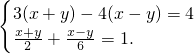
(3)解不等式组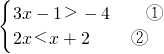 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来.
(1)解: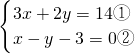
由②得,x=y+3③,
把③代入①得,3×(y+3)+2y=14,
解得,y=1,
把y=1代入③得,x=4.
∴原方程组的解是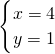 .
.
(2)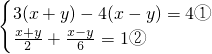
令x+y=a,x-y=b,
则原方程组可化为:
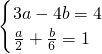 ,
,
解得,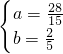 ,
,
则有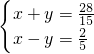 ,
,
解得
 .
.
(3)解:由①得x>-1,
由②得x<2,
∴原不等式组的解集是-1<x<2.
在数轴上表示为:
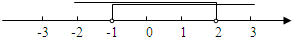
分析:(1)由于②中未知数x、y的系数为1和-1,可用代入法解答;
(2)由于两方程中都有x+y与x-y,可用换元法解答;
(3)分别求出不等式组中每个不等式的解集,再求其公共部分即可.
点评:本题主要考查了解一元一次不等式组和解一元一次方程组,(1)由于未知数系数较小,可选择代入法解答;(2)由于方程组中均含有x+y和x-y,可选用换元法;(3)分别求出不等式的解集,再根据“同大取较大,同小取较小,小大大小中间找,大大小小解不了”取其公共部分即可.
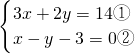
由②得,x=y+3③,
把③代入①得,3×(y+3)+2y=14,
解得,y=1,
把y=1代入③得,x=4.
∴原方程组的解是
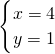 .
.(2)
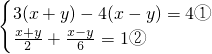
令x+y=a,x-y=b,
则原方程组可化为:
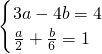 ,
,解得,
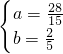 ,
,则有
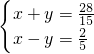 ,
,解得
 .
.(3)解:由①得x>-1,
由②得x<2,
∴原不等式组的解集是-1<x<2.
在数轴上表示为:
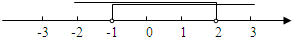
分析:(1)由于②中未知数x、y的系数为1和-1,可用代入法解答;
(2)由于两方程中都有x+y与x-y,可用换元法解答;
(3)分别求出不等式组中每个不等式的解集,再求其公共部分即可.
点评:本题主要考查了解一元一次不等式组和解一元一次方程组,(1)由于未知数系数较小,可选择代入法解答;(2)由于方程组中均含有x+y和x-y,可选用换元法;(3)分别求出不等式的解集,再根据“同大取较大,同小取较小,小大大小中间找,大大小小解不了”取其公共部分即可.

练习册系列答案
相关题目
 解下列方程组或不等式组
解下列方程组或不等式组