题目内容
求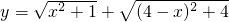 的最小值.
的最小值.
 解:利用数形结合,
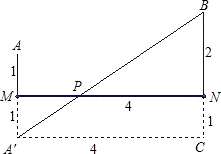
解:利用数形结合,如图,线段MN=4,
过A、B两点分别作AM⊥MN,
BN⊥MN,使AM=1,BN=2,
过点A作关于MN的轴对称点A′,
连接AB,交MN于点P,
则线段A′B即为所求的最小值.
过A′作A′C∥MN交BN延长线于C.
则A′C=4,BC=3,
在Rt△A′BC中,∠C=90°,
由勾股定理有:A′B2=A′C2+BC2,可得A′B=5,
所以原式的最小值为5.
分析:利用数形结合的思想,把x2+1、(4-x)2+4看成是勾股定理的形式,则可作线段MN=4,过A、B两点分别作AM⊥MN,BN⊥MN,使AM=1,BN=2,过点A作关于MN的轴对称点A′,连接AB,交MN于点P,则线段A′B即为所求的最小值,求解即可.
点评:此题难度较大,由二次根式被开方因式的特点作图是个难点.

练习册系列答案
相关题目
温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将 件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示。设安排
件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示。设安排 件产品运往A地。
件产品运往A地。
1.当 时①根据信息填表:
时①根据信息填表:
|
|
A地 |
B地 |
C地 |
合计 |
|
产品件数(件) |
|
|
|
200 |
|
运费(元) |
30 |
|
|
|
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
2.若总运费为5800元,求 的最小值。
的最小值。

 的值;
的值; 的最小值.
的最小值.
 的两个实数根,设过D, E,F三点的⊙O的面积为
的两个实数根,设过D, E,F三点的⊙O的面积为 ,矩形PDEF的面积为
,矩形PDEF的面积为

 的最小值;
的最小值; 的两个实数根,设过D, E,F三点的⊙O的面积为
的两个实数根,设过D, E,F三点的⊙O的面积为 ,矩形PDEF的面积为
,矩形PDEF的面积为

 的最小值;
的最小值; 的两个实数根,设过D, E,F三点的⊙O的面积为
的两个实数根,设过D, E,F三点的⊙O的面积为 ,矩形PDEF的面积为
,矩形PDEF的面积为

 的最小值;
的最小值;