题目内容
为了测量某河面的宽度，小陈同志设计了如下的测量方案：先在河的北岸选定一点A，再在河的南岸选定相距120米的两点B、C（如图）分别测得∠ABC=30°，∠ACB=60°，请你根据测得的数据，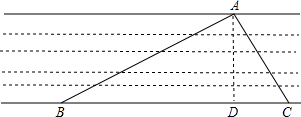
计算出河宽AD．（结果用根式表示）
解：在Rt△ADB中，∠ABD=30°，
∴BD=
，
在Rt△ADC中，∠ACD=60°，
∴CD=
AD，
又∵BC=120，
∴+AD=120，
解得AD=30
m．
答：河宽AD的长为30m．
分析：在解本题时，必须构建直角三角形，应该把特殊角60°，30°放到所构建的三角形中，利用三角函数解直角三角形即可．
点评：本题考查了解直角三角形的应用中的方向角问题，解本题关键是构建直角三角形，利用三角函数来解答．
∴BD=
，在Rt△ADC中，∠ACD=60°，
∴CD=
AD，又∵BC=120，
∴
+AD=120，解得AD=30
m．答：河宽AD的长为30
m．分析：在解本题时，必须构建直角三角形，应该把特殊角60°，30°放到所构建的三角形中，利用三角函数解直角三角形即可．
点评：本题考查了解直角三角形的应用中的方向角问题，解本题关键是构建直角三角形，利用三角函数来解答．
练习册系列答案
相关题目
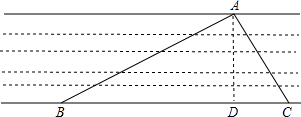计算出河宽AD．（结果用根式表示）
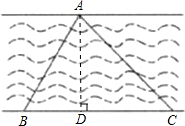为了测量汉江某段河面的宽度，秋实同学设计了如下图所示的测量方案：先在河的北岸选一定点A，再在河的南岸选定相距a米的两点B、C（如图），分别测得∠ABC=α，∠ACB=β，请你根据秋实同学测得的数据，计算出河宽AD．（结果用含a和含α、β的三角函数表示）
