题目内容
如图，在⊙O中，CD为⊙O的直径，
=
，点E为OD上任意一点（不与O、D重合）．
求证：AE=BE．
解：∵=，
∴∠AOC=∠BOC，
∴∠AOE=∠BOE，
∵OA、OB是⊙O的半径，
∴OA=OB，
在△AOE和△BOE中，
∴△AOE≌△BOE，
∴AE=BE．
分析：根据=，得出∠AOE=∠BOE，然后证明△AOE≌△BOE，即可得出结论．
点评：本题考查了圆周角定理及全等三角形的判定，属于基础题，得到∠AOE=∠BOE，是解答本题的关键．
=，∴∠AOC=∠BOC，
∴∠AOE=∠BOE，
∵OA、OB是⊙O的半径，
∴OA=OB，
在△AOE和△BOE中，
∴△AOE≌△BOE，
∴AE=BE．
分析：根据
=，得出∠AOE=∠BOE，然后证明△AOE≌△BOE，即可得出结论．点评：本题考查了圆周角定理及全等三角形的判定，属于基础题，得到∠AOE=∠BOE，是解答本题的关键．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
13、如图，在△ABC中，CD是AB边上的中线，线段AC比BC短2cm，则△BCD和△ACD的周长的差是
14、如图，在△ABC中，CD平分∠ACB，DE∥AC，DC∥EF，则与∠ACD相等角有
如图，在△ABC中，CD、BE分别是AB、AC边上的高，∠EBC=45°，BE=6，CD=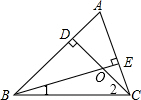
如图，在△ABC中，CD是AB边上的高，BE是AC边上的高，点O是两条高线的交点，则∠A与∠1+∠2的关系是（ ）
如图，在⊙O中，