题目内容
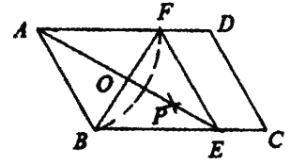
【题目】（操作观察）任意一张三角形纸片有3个顶点。
第1次在它的内部增画1个点，此时三角形纸片内部共有1个点；
第2次在它的内部继续增画2个点，此时三角形纸片内部共有1+2=3个点；
第3次在它的内部继续增画3个点，此时三角形纸片内部共有1+2+3=6个点；
……
第
次在它的内部继续增画个点，此时三角形纸片内部共有
个点。
（动手实践）
第次画点后，在三角形纸片内部共有个点，以
个点为顶点，把三角形纸片剪成若干个小三角形纸片，设最多可以剪得
个这样的小三角形。
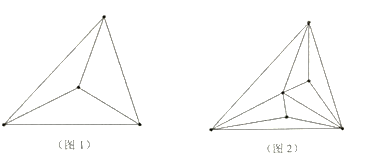
（思考解答）
（1）第次画点后，
__________________；（用含有的代数式表示）；
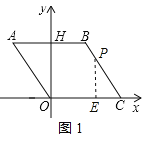
（2）第1次画点后，如图1，以4个点为顶点，将原三角形纸片剪成若干个小三角形，最多可以剪得3个这样的小三角形，所以
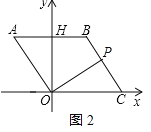
；第2次画点后，如图2，以6个点为顶点，最多可以剪得7个这样的小三角形，所以
；第3次画点后，以9个点为顶点，可得
____________________；
（3）第次画点后，可得
______________；（用含有的代数式表示）；
（4）第次画点后，可得个小三角形，第
次画点后，可得
个小三角形，则
________________________。（用含有的代数式表示）。
【答案】（1）
；（2）13；（3）
；（4）
【解析】
（1）根据题意
,用代数式表示即可；
（2）第2次画点后，在原基础上增加了2个点，就增加了
个小三角形，
，第3次画点后，在原基础上增加了3个点，就增加了
个小三角形，
，
（3）根据
，
，
，可以推出
；
（4）由（3）可推得
，两式相减，去括号化简即可求得.
（1）根据题意得：, 也可以写成
,
∴
(共有n个这样的数)
∴
故答案为：
（2）第3次画点后，在原基础上增加了3个点，就增加了个小三角形，，
故答案为：13；
（3）第4次画点后，在原基础上增加了4个点，就增加了
个小三角形，
，
根据，，，
，
∵
，
，
，
∴
故答案为：
（4）
故答案为：
