题目内容
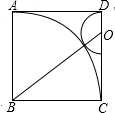 (2012•曲阜市模拟)如图,在正方形ABCD中,O是CD边上一点,以O为圆心,OD为半径的半圆恰好与以B为圆心,BC为半径的扇形的弧外切,则sin∠OBC的值为( )
(2012•曲阜市模拟)如图,在正方形ABCD中,O是CD边上一点,以O为圆心,OD为半径的半圆恰好与以B为圆心,BC为半径的扇形的弧外切,则sin∠OBC的值为( )分析:设正方形的边长是1,半圆的半径是x.根据两圆外切,则圆心距等于两圆半径之和表示OB的长,从而根据勾股定理求得x的值,进一步根据锐角三角函数的概念求解.
解答:解:设正方形的边长是1,半圆的半径是x.
则OB=1+x,OC=1-x.
在Rt△OBC中,根据勾股定理,得
(1+x)2=(1-x)2+1,
x=
.
则OB=
,OC=
.
则sin∠OBC=
=
.
故选:D.
则OB=1+x,OC=1-x.
在Rt△OBC中,根据勾股定理,得
(1+x)2=(1-x)2+1,
x=
| 1 |
| 4 |
则OB=
| 5 |
| 4 |
| 3 |
| 4 |
则sin∠OBC=
| OC |
| OB |
| 3 |
| 5 |
故选:D.
点评:此题主要考查了相切两圆的性质、勾股定理以及锐角三角函数的概念,得出半圆的半径是解题关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
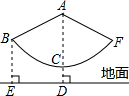 (2012•曲阜市模拟)如图,秋千拉绳长AB为3米,静止时踩板离地面0.5米,小朋友荡该秋千时,秋千在最高处时踩板离地面2米(左右对称),请计算该秋千所荡过的圆弧BF长是( )
(2012•曲阜市模拟)如图,秋千拉绳长AB为3米,静止时踩板离地面0.5米,小朋友荡该秋千时,秋千在最高处时踩板离地面2米(左右对称),请计算该秋千所荡过的圆弧BF长是( )