题目内容
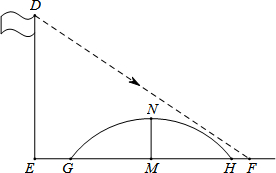
 如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
【答案】分析:根据已知得出旗杆高度,进而得出GM=MH,再利用勾股定理求出半径即可.
解答: 解:∵小刚身高1.6米,测得其影长为2.4米,
解:∵小刚身高1.6米,测得其影长为2.4米,
∴8米高旗杆DE的影子为:12m,
∵测得EG的长为3米,HF的长为1米,
∴GH=12-3-1=8(m),
∴GM=MH=4m.
如图,设小桥的圆心为O,连接OM、OG.
设小桥所在圆的半径为r,
∵MN=2m,
∴OM=(r-2)m.
在Rt△OGM中,由勾股定理得:
∴OG2=OM2+42,
∴r2=(r-2)2+16,
解得:r=5,
答:小桥所在圆的半径为5m.
点评:此题主要考查了垂径定理以及勾股定理的应用,根据已知得出关于r的等式是解题关键.
解答:
 解:∵小刚身高1.6米,测得其影长为2.4米,
解:∵小刚身高1.6米,测得其影长为2.4米,∴8米高旗杆DE的影子为:12m,
∵测得EG的长为3米,HF的长为1米,
∴GH=12-3-1=8(m),
∴GM=MH=4m.
如图,设小桥的圆心为O,连接OM、OG.
设小桥所在圆的半径为r,
∵MN=2m,
∴OM=(r-2)m.
在Rt△OGM中,由勾股定理得:
∴OG2=OM2+42,
∴r2=(r-2)2+16,
解得:r=5,
答:小桥所在圆的半径为5m.
点评:此题主要考查了垂径定理以及勾股定理的应用,根据已知得出关于r的等式是解题关键.

练习册系列答案
相关题目
 (2013•深圳)如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
(2013•深圳)如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
 如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.