题目内容
当抛物线y=ax2+bx+c与x轴两交点及抛物线上一点P组成以P为直角顶点的直角三角形时,则点P的坐标( )A.只与a有关
B.只与b有关
C.只与c有关
D.与a、b、c均有关
【答案】分析:设抛物线y=ax2+bx+c与x轴的交点A(x1,0),B(x2,0),抛物线上一点P(x,y).先由韦达定理得出x1+x2=-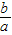 ,x1•x2=
,x1•x2=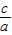 .再过P作PM⊥x轴于M,易证△APM∽△PBM,根据相似三角形对应边成比例得出PM2=BM×AM,即y2=(x2-x)•(x-x1),然后由点P是抛物线y=ax2+bx+c上的一点,将y=ax2+bx+c代入,整理后得出y=-
.再过P作PM⊥x轴于M,易证△APM∽△PBM,根据相似三角形对应边成比例得出PM2=BM×AM,即y2=(x2-x)•(x-x1),然后由点P是抛物线y=ax2+bx+c上的一点,将y=ax2+bx+c代入,整理后得出y=-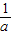 ,x=
,x= ,即可判断.
,即可判断.
解答: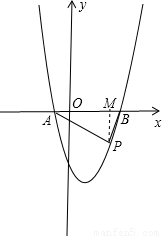 解:设抛物线y=ax2+bx+c与x轴的交点A(x1,0),B(x2,0),抛物线上一点P(x,y).
解:设抛物线y=ax2+bx+c与x轴的交点A(x1,0),B(x2,0),抛物线上一点P(x,y).
∵点A、B是抛物线y=ax2+bx+c与x轴交点,
∴x1,x2是方程ax2+bx+c=0的两个根,则由韦达定理x1+x2=-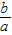 ,x1•x2=
,x1•x2=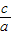 .
.
过P作PM⊥x轴于M,
∵A(x1,0),B(x2,0),P(x,y),
∴PM=|y|,BM=x2-x,AM=x-x1.
∵在△PAB中,∠APB=90°,PM⊥AB,
∴∠PMA=∠PMB=90°,
∴∠PAB+∠PBA=90°,∠PBA+∠BPM=90°,
∴∠BPM=∠PAB,
∴△APM∽△PBM,
∴ =
= ,
,
∴PM2=BM×AM,
∴y2=(x2-x)•(x-x1),
整理得:x2-(x1+x2)x+x1•x2+y2=x2+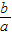 •x+
•x+ +y2=0,
+y2=0,
即x2+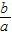 •x+
•x+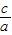 +y2=0,
+y2=0,
两边同时乘以a,得ax2+b•x+c+ay2=0,
∵点P是抛物线y=ax2+bx+c上的一点,
所以y=ax2+bx+c,
∴将其代入ax2+b•x+c+ay2=0,得
y+ay2=0,
即y•(1+ay)=0.
∵点P不与点A、B重合,
∴y≠0,
∴y=- ,
,
∴x= .
.
故选D.
点评:本题考查了抛物线与x轴的交点,相似三角形的判定与性质,韦达定理,解一元二次方程,难度较大.
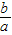 ,x1•x2=
,x1•x2=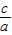 .再过P作PM⊥x轴于M,易证△APM∽△PBM,根据相似三角形对应边成比例得出PM2=BM×AM,即y2=(x2-x)•(x-x1),然后由点P是抛物线y=ax2+bx+c上的一点,将y=ax2+bx+c代入,整理后得出y=-
.再过P作PM⊥x轴于M,易证△APM∽△PBM,根据相似三角形对应边成比例得出PM2=BM×AM,即y2=(x2-x)•(x-x1),然后由点P是抛物线y=ax2+bx+c上的一点,将y=ax2+bx+c代入,整理后得出y=-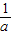 ,x=
,x= ,即可判断.
,即可判断.解答:
 解:设抛物线y=ax2+bx+c与x轴的交点A(x1,0),B(x2,0),抛物线上一点P(x,y).
解:设抛物线y=ax2+bx+c与x轴的交点A(x1,0),B(x2,0),抛物线上一点P(x,y).∵点A、B是抛物线y=ax2+bx+c与x轴交点,
∴x1,x2是方程ax2+bx+c=0的两个根,则由韦达定理x1+x2=-
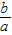 ,x1•x2=
,x1•x2=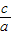 .
.过P作PM⊥x轴于M,
∵A(x1,0),B(x2,0),P(x,y),
∴PM=|y|,BM=x2-x,AM=x-x1.
∵在△PAB中,∠APB=90°,PM⊥AB,
∴∠PMA=∠PMB=90°,
∴∠PAB+∠PBA=90°,∠PBA+∠BPM=90°,
∴∠BPM=∠PAB,
∴△APM∽△PBM,
∴
 =
= ,
,∴PM2=BM×AM,
∴y2=(x2-x)•(x-x1),
整理得:x2-(x1+x2)x+x1•x2+y2=x2+
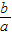 •x+
•x+ +y2=0,
+y2=0,即x2+
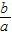 •x+
•x+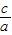 +y2=0,
+y2=0,两边同时乘以a,得ax2+b•x+c+ay2=0,
∵点P是抛物线y=ax2+bx+c上的一点,
所以y=ax2+bx+c,
∴将其代入ax2+b•x+c+ay2=0,得
y+ay2=0,
即y•(1+ay)=0.
∵点P不与点A、B重合,
∴y≠0,
∴y=-
 ,
,∴x=
 .
.故选D.
点评:本题考查了抛物线与x轴的交点,相似三角形的判定与性质,韦达定理,解一元二次方程,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知抛物线y=ax2+b(a>0,b>0),函数y=b|x|
已知抛物线y=ax2+b(a>0,b>0),函数y=b|x|