题目内容
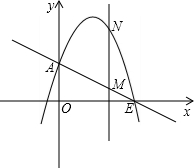
如图,一次函数y=-
x+2分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
| 1 |
| 2 |
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?

(1)∵一次函数y=-
x+2分别交y轴、x轴于A、B两点,
∴x=0时,y=2,y=0时,x=4,
∴A(0,2),B(4,0),
将x=0,y=2代入y=-x2+bx+c得c=2,
将x=4,y=0,c=2代入y=-x2+bx+c,
得到b=
,
∴y=-x2+
x+2;
(2)∵作垂直x轴的直线x=t,在第一象限交直线AB于M,
∴由题意,易得M(t,-
t+2),N(t,-t2+
t+2),
从而得到MN=-t2+
t+2-(-
t+2)=-t2+4t(0<t<4),
当t=-
=2时,MN有最大值为:
=4.
| 1 |
| 2 |
∴x=0时,y=2,y=0时,x=4,
∴A(0,2),B(4,0),
将x=0,y=2代入y=-x2+bx+c得c=2,

将x=4,y=0,c=2代入y=-x2+bx+c,
得到b=
| 7 |
| 2 |
∴y=-x2+
| 7 |
| 2 |
(2)∵作垂直x轴的直线x=t,在第一象限交直线AB于M,
∴由题意,易得M(t,-
| 1 |
| 2 |
| 7 |
| 2 |
从而得到MN=-t2+
| 7 |
| 2 |
| 1 |
| 2 |
当t=-
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
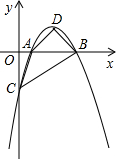
 值,若不存在请说明理由.
值,若不存在请说明理由.

 园的面积最大?最大面积是多少?
园的面积最大?最大面积是多少?