题目内容
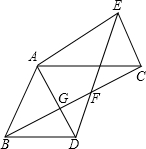如图，在△ABD和△ADE中，AB=AD，AC=AE，∠BAD=∠CAE，连接BC、DE相交于点F，BC与AD相交于点G（1）试判断线段BC、DE的数量关系，并说明理由；
（2）如果∠ABC=∠CBD，那么线段FD是线段FG和FB的比例中项吗？为什么？
分析：（1）利用SAS证明△ABC≌△ADE，得BC=DE．
（2）根据（1）里的全等关系，可证出△BFD∽△DFG，所以
=
，即FD2=FG•FB．
（2）根据（1）里的全等关系，可证出△BFD∽△DFG，所以
| BF |
| DF |
| DF |
| GF |
解答：解：（1）BC、DE的数量关系是BC=DE．
理由如下：∵∠BAD=∠CAE，
∴∠BAD+∠DAC=∠CAE+∠DAC，即∠BAC=∠DAE，
又∵AB=AD，AC=AE，
∴△ABC≌△ADE．（SAS）
∴BC=DE．
（2）线段FD是线段FG和FB的比例中项．
理由如下：∵△ABC≌△ADE，∴∠ABC=∠ADE．
∵∠ABC=∠CBD，∴∠ADE=∠CBD，
又∵∠BFD=∠DFG，
∴△BFD∽△DFG．
∴
=
∴FD2=FG•FB．
即线段FD是线段FG和FB的比例中项．
理由如下：∵∠BAD=∠CAE，
∴∠BAD+∠DAC=∠CAE+∠DAC，即∠BAC=∠DAE，
又∵AB=AD，AC=AE，
∴△ABC≌△ADE．（SAS）
∴BC=DE．
（2）线段FD是线段FG和FB的比例中项．
理由如下：∵△ABC≌△ADE，∴∠ABC=∠ADE．
∵∠ABC=∠CBD，∴∠ADE=∠CBD，
又∵∠BFD=∠DFG，
∴△BFD∽△DFG．
∴
| BF |
| DF |
| DF |
| GF |
即线段FD是线段FG和FB的比例中项．
点评：本题利用了全等三角形的判定和性质，以及相似三角形的判定和性质．
练习册系列答案
相关题目
24、如图，在△ABD和△ACE中，有下列四个等式：①AB=AC；②AD=AE；③∠1=∠2；④BD=CE．以其中三个条件为题设，填入已知栏中，一个论断为结论，填入下面求证栏中，使之组成一个真命题，并写出证明过程．
如图，在△ABD和△ACE中，AB=AD，AC=AE，∠BAD=∠CAE，连接BC、DE相交于点F，BC与AD相交于点G．求证：BC=DE．
如图，在△ABD和△BAC中，∠1=∠2，∠C=∠D，AC、BD相交于点E，则下列结论中正确的个数有（ ）
如图，在△ABD和△ACE中，AB=AD，AC=AE，∠BAD=∠CAE，连接BC、DE相交于点F，BC与AD相交于点G．
如图，在△ABD和△ACE中，有下列四个等式：