题目内容
将点P（2，1）绕坐标原点O顺时针旋转90°后得到点P′的坐标为
（1，-2）
（1，-2）
．分析：过P作PC⊥y轴于C，过P′作P′D⊥y轴于D，根据旋转求出∠P=∠P′OD，证△PC0≌△ODP′，推出P′D=OC=1，OD=CP=2即可．
解答：
解：过P作PC⊥y轴于C，过P′作P′D⊥y轴于D．
∵∠POP′=90°，∠PCO=90°，
∴∠POC+∠P′OD=90°，∠P+∠POC=90°，
∴∠P=∠P′OD，
∵∠PCO=∠P′DO=90°，OP=OP′，
∴△PC0≌△ODP′，
∴P′D=OC=1，OD=CP=2，
∴P′的坐标是（1，-2）．
故答案为：（1，-2）．
解：过P作PC⊥y轴于C，过P′作P′D⊥y轴于D．∵∠POP′=90°，∠PCO=90°，
∴∠POC+∠P′OD=90°，∠P+∠POC=90°，
∴∠P=∠P′OD，
∵∠PCO=∠P′DO=90°，OP=OP′，
∴△PC0≌△ODP′，
∴P′D=OC=1，OD=CP=2，
∴P′的坐标是（1，-2）．
故答案为：（1，-2）．
点评：本题主要考查对坐标与图形变换-旋转，全等三角形的性质和判定等知识点的理解和掌握，能正确画出图形并求出△PC0≌△ODP′是解此题的关键．
练习册系列答案
相关题目
在平面直角坐标系中，△ABC的顶点坐标是A（-2，3），B（-4，-1），C（2，0）．点P（m，n）为△ABC内一点，平移△ABC得到△A1B1C1，使点A1（2，-3）．
（m，n）为△ABC内一点，平移△ABC得到△A1B1C1，使点P（m，n）移到P（m+6，n+1）处．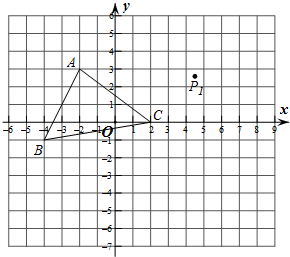
（m，n）为△ABC内一点，平移△ABC得到△A1B1C1，使点P（m，n）移到P（m+6，n+1）处．
