题目内容
结合所给的图形，编一道几何证明题，证明四边形AEDF是菱形，并利用所给的条件，写出“已知”“求证”和“证明”的过程。
解：已知，如图，AD是△ABC的角平分线，DE∥AC，ED=AF，求证：四边形AEDF是菱形。
证明：∵AD是△ABC的角平分线
∴∠EAD=∠FAD
∵DE∥AC，ED=AF
∴四边形AEDF是平行四边形
∴∠EAD=∠ADF
∴∠FAD=∠FDA
∴AF=DF
∴四边形AEDF是菱形。（答案不唯一）
证明：∵AD是△ABC的角平分线
∴∠EAD=∠FAD
∵DE∥AC，ED=AF
∴四边形AEDF是平行四边形
∴∠EAD=∠ADF
∴∠FAD=∠FDA
∴AF=DF
∴四边形AEDF是菱形。（答案不唯一）
练习册系列答案
相关题目
如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：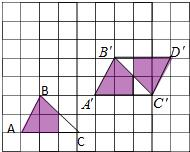
如图，在方格纸（每个小方格都是边长为1个单位长度的正方形）上，并且图形的顶点均在格点上，请结合所给的方格纸解答下列问题：
如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：