题目内容
(1)x2-4x+1=0(配方法)
(2)3x2-1=4x(公式法)
(3)9(2x-5)2-4=0
(4)x(x-1)=x
(5)2x2-x-15=0
(6)2x2-7x-4=0(用配方法)
(7)x2=2x
(8)x2-2 x+2=0(公式法)
x+2=0(公式法)
解:(1)x2-4x+4=3,
(x-2)2=3,
x-2=± ,
,
所以x1=2+ ,x2=2-
,x2=2- ;
;
(2))3x2-4x-1=0,
△=16-4×3×(-1)=28,
x= =
= ,
,
所以x1= ,x2=
,x2= ;
;
(3)9(2x-5)2=4,
3(2x-5)=±2,
所以x1=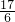 ,x2=
,x2= ;
;
(4)x(x-1)-x=0,
x(x-1-1)=0,
x=0或x-1-1=0,
所以x1=0,x2=2;
(5)(2x+5)(x-3)=0,
2x+5=0或x-3=0,
所以x1=- ,x2=3;
,x2=3;
(6)x2- x=2,
x=2,
x2- x+
x+ =2+
=2+
(x- )2=
)2= ,
,
x- =±
=± ,
,
所以x1=4,x2=- ;
;
(7)x2-2x=0,
x(x-2)=0,
x=0或x-2=0,
所以x1=0,x2=2;
(8)△=20-4×2=12,
x= =
= ±
± ,
,
所以x1= +
+ ,x2=
,x2= -
- .
.
分析:(1)、(6)利用配方法解方程;
(2)、(8)利用公式法解方程;
(3)利用直接开平方法解方程;
(4)、(5)、(7)利用因式分解法解方程.
点评:本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了直接开平方法、配方法和公式法解一元二次方程.
(x-2)2=3,
x-2=±
 ,
,所以x1=2+
 ,x2=2-
,x2=2- ;
;(2))3x2-4x-1=0,
△=16-4×3×(-1)=28,
x=
 =
= ,
,所以x1=
 ,x2=
,x2= ;
;(3)9(2x-5)2=4,
3(2x-5)=±2,
所以x1=
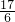 ,x2=
,x2= ;
;(4)x(x-1)-x=0,
x(x-1-1)=0,
x=0或x-1-1=0,
所以x1=0,x2=2;
(5)(2x+5)(x-3)=0,
2x+5=0或x-3=0,
所以x1=-
 ,x2=3;
,x2=3;(6)x2-
 x=2,
x=2,x2-
 x+
x+ =2+
=2+
(x-
 )2=
)2= ,
,x-
 =±
=± ,
,所以x1=4,x2=-
 ;
;(7)x2-2x=0,
x(x-2)=0,
x=0或x-2=0,
所以x1=0,x2=2;
(8)△=20-4×2=12,
x=
 =
= ±
± ,
,所以x1=
 +
+ ,x2=
,x2= -
- .
.分析:(1)、(6)利用配方法解方程;
(2)、(8)利用公式法解方程;
(3)利用直接开平方法解方程;
(4)、(5)、(7)利用因式分解法解方程.
点评:本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了直接开平方法、配方法和公式法解一元二次方程.

练习册系列答案
相关题目
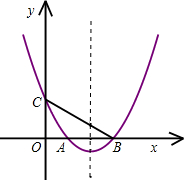 与原抛物线交于点M,当△MA′B′的面积为
与原抛物线交于点M,当△MA′B′的面积为