题目内容
 (2013•房山区二模)已知抛物线y=(3-m)x2+2(m-3)x+4m-m2的最低点A的纵坐标是3,直线y=mx+b经过点A,与y轴交于点B,与x轴交于点C.
(2013•房山区二模)已知抛物线y=(3-m)x2+2(m-3)x+4m-m2的最低点A的纵坐标是3,直线y=mx+b经过点A,与y轴交于点B,与x轴交于点C.(1)求抛物线与直线AB的解析式.
(2)将直线AB绕点O顺时针旋转90°,与x轴交于点D,与y轴交于点E,求sin∠BDE的值.
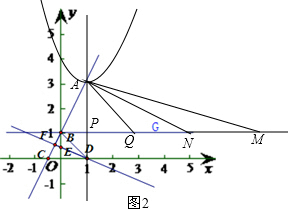
(3)过B点作x轴的平行线BG,点M在直线BG上,且到抛物线的对称轴的距离为6,设点N在直线BG上,请你直接写出使得∠AMB+∠ANB=45°的点N的坐标.
分析:(1)先由y=(3-m)x2+2(m-3)x+4m-m2可以求出抛物线的对称轴,就可以求出顶点坐标,代入解析式就可以求出m的值,将A的坐标及m的值代入一次函数的解析式就可以求出结论;
(2)根据旋转的性质就可以求出D、E的坐标,由勾股定理就可以求出BD,DE、DF的值根据求锐角三角函数的方法就可以求出结论;
(3)根据题意画出图形,分情况讨论运用相似三角形的性质就可以求出结论.
(2)根据旋转的性质就可以求出D、E的坐标,由勾股定理就可以求出BD,DE、DF的值根据求锐角三角函数的方法就可以求出结论;
(3)根据题意画出图形,分情况讨论运用相似三角形的性质就可以求出结论.
解答:解:(1)∵y=(3-m)x2+2(m-3)x+4m-m2的,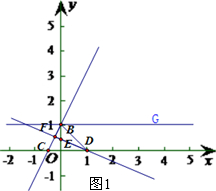
∴抛物线的对称轴x=-
=-
=1.
∵抛物线y=(3-m)x2+2(m-3)x+4m-m2的最低点A的纵坐标是3
∴抛物线的顶点为A(1,3)
∴m2-5m+6=0,
∴m=3或m=2,
∵3-m>0,
∴m<3
∴m=2,
∴抛物线的解析式为:y=x2-2x+4,
直线为y=2x+b.
∵直线y=mx+b经过点A(1,3)
∴3=2+b,
∴b=1.
∴直线AB为:y=2x+1;
(2)令x=0,则y=1,)令y=0,则x=-
,
∴B(0,1),C(-
,0)
将直线AB绕O点顺时针旋转900,设DE与BC交于点F
∴D(1,0),E(0,
),∠CFD=90°,
∴OB=OD=1 OC=
,∴CD=
在Rt△BOC中,由勾股定理,得
CB=
,BD=
.
∵CD•OB=CB•DF,
∴DF=
,
∴由勾股定理,得
BF=
,
∴Sin∠BDE=
=
=
;
(3)如图2,在BG上取一点Q,使AP=QP,
∴∠AQP=45°.
∴∠ANB+∠QAN=∠QAM+∠AMB=45°.
∵∠AMB+∠ANB=45°,
∴∠ANB=∠QAM,
∴△AQN∽△MQA,
∴
=
.
∵AD=3,OD=1,
∴AP=QP=2,
∴QM=4,AQ=2
,
∵MP=6,
∴MQ=4.
∴
=
,
∴QN=2,
∴BN=5.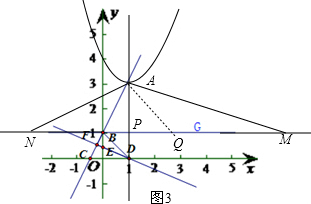
∴N(5,1);
如图3,在BG上取一点Q,使AP=QP,
∴∠AQP=45°.
∴∠ANB+∠AMB=∠QAM+∠AMB=45°.
∴∠ANB=∠QAM,
∴△AQM∽△NAM,
∴
=
.
∵AD=3,OD=1,
∴AP=QP=2,
∴QM=4,BM=7,AQ=2
,
∵MP=6,
∴MQ=4.AM=2
,
∴
=
,
∴MN=10,
∴BN=3.
∴N(-3,1);
∴N(-3,1)或(5,1).

∴抛物线的对称轴x=-
| b |
| 2a |
| 2(m-3) |
| 2(3-m) |
∵抛物线y=(3-m)x2+2(m-3)x+4m-m2的最低点A的纵坐标是3
∴抛物线的顶点为A(1,3)
∴m2-5m+6=0,
∴m=3或m=2,
∵3-m>0,
∴m<3
∴m=2,
∴抛物线的解析式为:y=x2-2x+4,
直线为y=2x+b.
∵直线y=mx+b经过点A(1,3)
∴3=2+b,
∴b=1.
∴直线AB为:y=2x+1;
(2)令x=0,则y=1,)令y=0,则x=-
| 1 |
| 2 |
∴B(0,1),C(-
| 1 |
| 2 |
将直线AB绕O点顺时针旋转900,设DE与BC交于点F
∴D(1,0),E(0,
| 1 |
| 2 |
∴OB=OD=1 OC=
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△BOC中,由勾股定理,得
CB=
| ||
| 2 |
| 2 |
∵CD•OB=CB•DF,
∴DF=
| 3 |
| 5 |
| 5 |
∴由勾股定理,得
BF=
| ||
| 5 |

∴Sin∠BDE=
| BF |
| BD |
| ||||
|
| ||
| 10 |
(3)如图2,在BG上取一点Q,使AP=QP,
∴∠AQP=45°.
∴∠ANB+∠QAN=∠QAM+∠AMB=45°.
∵∠AMB+∠ANB=45°,
∴∠ANB=∠QAM,
∴△AQN∽△MQA,
∴
| AQ |
| MQ |
| QN |
| QA |
∵AD=3,OD=1,
∴AP=QP=2,
∴QM=4,AQ=2
| 2 |
∵MP=6,
∴MQ=4.
∴
2
| ||
| 4 |
| QN | ||
2
|
∴QN=2,
∴BN=5.

∴N(5,1);
如图3,在BG上取一点Q,使AP=QP,
∴∠AQP=45°.
∴∠ANB+∠AMB=∠QAM+∠AMB=45°.
∴∠ANB=∠QAM,
∴△AQM∽△NAM,
∴
| AM |
| MN |
| QM |
| AM |
∵AD=3,OD=1,
∴AP=QP=2,
∴QM=4,BM=7,AQ=2
| 2 |
∵MP=6,
∴MQ=4.AM=2
| 10 |
∴
2
| ||
| MN |
| 4 | ||
2
|
∴MN=10,
∴BN=3.
∴N(-3,1);
∴N(-3,1)或(5,1).
点评:本题考查了运用抛物线的顶点式求顶点坐标的运,运用待定系数法求出二次函数与一次函数的解析式的运用,旋转的性质的运用,相似三角形的判定及性质的运用,解答时寻找解答本题的突破口从抛物线的顶点入手,求N的坐标运用相似三角形的性质是关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 (2013•房山区二模)如图:⊙A、⊙B、⊙C两两不相交,且半径均为1,则图中三个阴影扇形的面积之和为( )
(2013•房山区二模)如图:⊙A、⊙B、⊙C两两不相交,且半径均为1,则图中三个阴影扇形的面积之和为( )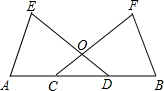 (2013•房山区二模)已知:如图,点C、D在线段AB上,E、F在AB同侧,DE与CF相交于点O,且AC=BD,AE=BF,∠A=∠B.求证:DE=CF.
(2013•房山区二模)已知:如图,点C、D在线段AB上,E、F在AB同侧,DE与CF相交于点O,且AC=BD,AE=BF,∠A=∠B.求证:DE=CF.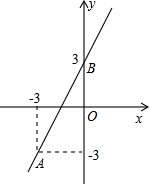 (2013•房山区二模)如图,直线AB过点A,且与y轴交于点B.
(2013•房山区二模)如图,直线AB过点A,且与y轴交于点B.