题目内容
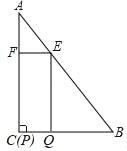
【题目】如图，Rt△ABC中，AB＝9，BC＝6，∠B＝90°，将△ABC折叠，使A点与BC的中点D重合，折痕为PQ，则△PQD的面积为（ ）
A.
B.
C.
D.
【答案】D
【解析】
由折叠的性质可得AQ＝QD，AP＝PD，由勾股定理可求AQ的长，由锐角三角函数分别求出AP，HQ的长，即可求解．
解：过点D作DN⊥AC于N，
∵点D是BC中点，
∴BD＝3，
∵将△ABC折叠，
∴AQ＝QD，AP＝PD，
∵AB＝9，BC＝6，∠B＝90°，
∴AC＝
，
∵sin∠C＝
＝
，
∴DN＝
，
∵cos∠C＝
，
∴CN＝
，
∴AN＝
，
∵PD2＝PN2+DN2，
∴AP2＝（﹣AP）2+
，
∴AP＝
，
∵QD2＝DB2+QB2，
∴AQ2＝（9﹣AQ）2+9，
∴AQ＝5，
∵sin∠A＝
＝
，
∴HQ＝
＝
∵∴△PQD的面积＝△APQ的面积＝
××＝
，
故选：D．
练习册系列答案
阅读快车系列答案
相关题目
