Question

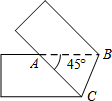（2013•徐州模拟）如图，将宽为1cm的纸条沿BC折叠，使∠CAB=45°，则折叠后重叠部分的面积为（　　）

• A．

  2

  cm²
• B．

  2

  2

  cm²
• C．

  3

  2

  cm²
• D．

  3

  cm²

Answer 1

分析：先根据题意得出△ABC是一个顶角为45°的等腰三角形，即∠A=45°，AC=AB，过C作CD⊥AB，垂足为D，根据三角函数定义求出AC，AB，然后就可以求出△ABC面积．

解答：解：∵纸条的两边互相平行，
∴∠1=∠BAC=45°，
∴∠ABC=

180°-∠1

2

=

180°-45°

2

=67.5°，
同理可得，∠ACB=67.5°，
∴△ABC是一个顶角为45°的等腰三角形，即∠A=45°，AC=AB．
作CD⊥AB，垂足为D，则CD=1．
∵sin∠A=

CD

AC

，
∴AC=

1

sin45°

=

2

=AB，
∴S_△ABC=

1

2

×AB×CD=

2

2

，
∴折叠后重叠部分的面积为

2

2

cm²．
故选B．

点评：本题考查的是图形折叠的性质，熟知图形翻折不变性的性质是解答此题的关键．