题目内容
 如图,在一次数学应用活动中,小明沿一条南北公路向北行走,在A处,他测得左边建筑C在北偏西30°方向,右边建筑D在北偏东30°方向;从A出向北40米行至B处,他又测得左边建筑物C在北偏西60°方向,右边建筑物D在北偏东45°方向.请根据以上数据求两建筑物C、D到这条南北公路的距离.
如图,在一次数学应用活动中,小明沿一条南北公路向北行走,在A处,他测得左边建筑C在北偏西30°方向,右边建筑D在北偏东30°方向;从A出向北40米行至B处,他又测得左边建筑物C在北偏西60°方向,右边建筑物D在北偏东45°方向.请根据以上数据求两建筑物C、D到这条南北公路的距离.
(参考数据: ≈1.732
≈1.732  ≈1.414,结果精确到0.1米)
≈1.414,结果精确到0.1米)
解:过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
 ,
,
在Rt△ACE中,可得AE= ,
,
在Rt△CBE中,BE= ,则
,则 -
- =AB=40米,
=AB=40米,
解得:CE=20 ≈34.6米;
≈34.6米;
同理:求得DF=20( +1)≈54.6米.
+1)≈54.6米.
答:C、D距公路的距离为34.6米、54.6米.
分析:过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,分别求出AE、AF的长度,继而根据AB=40米,可得出方程,解出即可.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数值的知识求出相关线段的长度,难度一般.
 ,
,在Rt△ACE中,可得AE=
 ,
,在Rt△CBE中,BE=
 ,则
,则 -
- =AB=40米,
=AB=40米,解得:CE=20
 ≈34.6米;
≈34.6米;同理:求得DF=20(
 +1)≈54.6米.
+1)≈54.6米.答:C、D距公路的距离为34.6米、54.6米.
分析:过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,分别求出AE、AF的长度,继而根据AB=40米,可得出方程,解出即可.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数值的知识求出相关线段的长度,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、某校对初三学生进行了一次数学应用问题小测验,如图是将(1)班60名同学的成绩进行整理后,分成5组画出的频率分布直方图.已知从左到右四个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次测验中成绩优秀(分数大于或等于80分为优秀)的有
23、某校对初三学生进行了一次数学应用问题小测验,如图是将(1)班60名同学的成绩进行整理后,分成5组画出的频率分布直方图.已知从左到右四个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次测验中成绩优秀(分数大于或等于80分为优秀)的有




 ≈1.73)
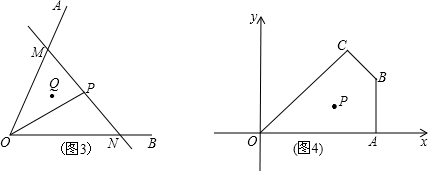
≈1.73) 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.