题目内容
抛物线y=2x2+6x+c与x轴的一个交点为（1，0），则这个抛物线的顶点坐标是 ．
【答案】分析：由于抛物线y=2x2+6x+c与x轴的一个交点为（1，0），代入解析式即可得到c=-8，从而求出解析式是：y=2x2+6x-8，再利用y=ax2+bx+c的顶点坐标公式（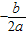
，
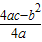）就可以得到顶点坐标．
解答：解：∵抛物线y=2x2+6x+c与x轴的一个交点为（1，0）
即抛物线经过点（1，0）
代入解析式得到c=-8
∴解析式是y=2x2+6x-8
∵y=ax2+bx+c的顶点坐标公式为（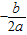
，
）
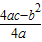代入公式求值得到顶点坐标是（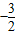
，-
）
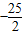故填空答案：（-
，-
）．
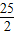点评：本题主要是对抛物线一般形式中对称轴，顶点坐标求法的考查，是中考中经常出现的问题．
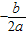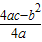，）就可以得到顶点坐标．解答：解：∵抛物线y=2x2+6x+c与x轴的一个交点为（1，0）
即抛物线经过点（1，0）
代入解析式得到c=-8
∴解析式是y=2x2+6x-8
∵y=ax2+bx+c的顶点坐标公式为（
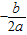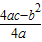，）代入公式求值得到顶点坐标是（
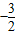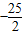，-）故填空答案：（-
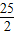，-）．点评：本题主要是对抛物线一般形式中对称轴，顶点坐标求法的考查，是中考中经常出现的问题．
练习册系列答案
一线名师权威作业本系列答案
相关题目