题目内容
在直角坐标系中,原点O到直线y=-| 3 | 4 |
分析:求得直线与两坐标轴的交点坐标,然后利用勾股定理求得两交点之间的距离,利用面积相等求得原点到直线的距离.
解答:解:令y=0,得:-
x+3=0,
解得:x=4,
令x=0得y=3,
∴直线与坐标轴的交点为(4,0),(0,3),
利用勾股定理得:
两交点之间的距离为
=5,
∴原点到直线的距离为
=2.4.
故答案为2.4.
| 3 |
| 4 |
解得:x=4,
令x=0得y=3,
∴直线与坐标轴的交点为(4,0),(0,3),
利用勾股定理得:
两交点之间的距离为
| 32+42 |
∴原点到直线的距离为
| 3×4 |
| 5 |
故答案为2.4.
点评:本题考查了一次函数与两坐标轴的交点坐标的求法,另外还考查了勾股定理的知识,特别是面积相等求直角三角形斜边上的高更是经常考查的内容之一.

练习册系列答案
相关题目
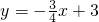 的距离是________.
的距离是________. 的距离是( )。
的距离是( )。