题目内容
①计算:22+ -3-1+
-3-1+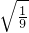 +(π-3.14)0; ②解方程:
+(π-3.14)0; ②解方程: .
.
解:(1)原式=4+(+4)-
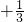 +1
+1
=8-0+1
=9;
(2)方程两边同乘以最简公分母(x+3)(x-2)得:x(x-2)=(x+3)+(x+3)(x-2),
整理得:x2-2x=x+3+x2+x-6,
∴-4x=-3,
∴x= ,
,
检验:当x= 时,(x+3)(x-2)=
时,(x+3)(x-2)=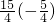 =
=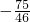 ≠0,
≠0,
所以,x= 是原方程的解.
是原方程的解.
分析:(1)首先进行乘方运算,开方运算,负整数指数幂的运算,零指数幂的运算,最后进行加减计算即可;
(2)方程两边同乘以最简公分母(x+3)(x-2),把分式方程转化为整式方程,求解即可,最后要把x的值代入到最简公分母进行检验.
点评:本题主要考查解分式方程,负整数指数幂、零指数幂、实数的运算,关键在于正确的运用相关的运算法则,找到分式方程的最简公分母,对分式方程进行化简,认真正确地进行计算即可.

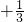 +1
+1=8-0+1
=9;
(2)方程两边同乘以最简公分母(x+3)(x-2)得:x(x-2)=(x+3)+(x+3)(x-2),
整理得:x2-2x=x+3+x2+x-6,
∴-4x=-3,
∴x=
 ,
,检验:当x=
 时,(x+3)(x-2)=
时,(x+3)(x-2)=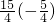 =
=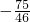 ≠0,
≠0,所以,x=
 是原方程的解.
是原方程的解.分析:(1)首先进行乘方运算,开方运算,负整数指数幂的运算,零指数幂的运算,最后进行加减计算即可;
(2)方程两边同乘以最简公分母(x+3)(x-2),把分式方程转化为整式方程,求解即可,最后要把x的值代入到最简公分母进行检验.
点评:本题主要考查解分式方程,负整数指数幂、零指数幂、实数的运算,关键在于正确的运用相关的运算法则,找到分式方程的最简公分母,对分式方程进行化简,认真正确地进行计算即可.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目