题目内容
 折叠Rt△ABC,使直角顶点C与斜边上的点D重合,AE为折痕,如图.已知AC=2CE,则BC:CA:AB=
折叠Rt△ABC,使直角顶点C与斜边上的点D重合,AE为折痕,如图.已知AC=2CE,则BC:CA:AB=分析:设EC=ED=x,BD=y,然后利用△BDE∽△BCA得到BE的表达式,利用勾股定理求得x、y的关系式,然后用x表示出BC、AC、AB的长,再求比值即可.
解答:解:设EC=ED=x,BD=y,则AC=AD=2x,
∵∠DBE=∠CBA,∠EDB=∠C=90°,
∴△BDE∽△BCA,
∴BD:BC=BE:AB=DE:AC,
∵EC=ED,AC=2CE,
∴BD:BC=BE:AB=DE:AC=1:2,
∴DB=
BC=y,
即BC=2y,
在Rt△ABC中
(2x)2+(2y)2=(2x+y)2,
∴y=
x,
∴BC=2y=
x,AB=2x+
x=
x,
∴BC:CA:AB=
x:2x:
x=4:3:5.
∵∠DBE=∠CBA,∠EDB=∠C=90°,
∴△BDE∽△BCA,
∴BD:BC=BE:AB=DE:AC,
∵EC=ED,AC=2CE,
∴BD:BC=BE:AB=DE:AC=1:2,
∴DB=
| 1 |
| 2 |
即BC=2y,
在Rt△ABC中
(2x)2+(2y)2=(2x+y)2,
∴y=
| 4 |
| 3 |
∴BC=2y=
| 8 |
| 3 |
| 4 |
| 3 |
| 10 |
| 3 |
∴BC:CA:AB=
| 8 |
| 3 |
| 10 |
| 3 |
点评:此题综合性强,综合利用了折叠的性质、勾股定理、相似三角形的判定等知识点,并运用了方程思想.

练习册系列答案
相关题目
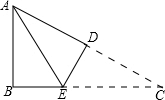 如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与点A重合,折痕为DE,求CE的长.
如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与点A重合,折痕为DE,求CE的长. 折叠Rt△ABC,使直角顶点C与斜边上的点D重合,AE为折痕,如图.已知AC=2CE,则BC:CA:AB=________.
折叠Rt△ABC,使直角顶点C与斜边上的点D重合,AE为折痕,如图.已知AC=2CE,则BC:CA:AB=________.
