题目内容
如图，已知双曲线
经过直角三角形OAB斜边OB的中点D，与直角边AB相交于点C．若△OBC的面积为3，则k= .
经过直角三角形OAB斜边OB的中点D，与直角边AB相交于点C．若△OBC的面积为3，则k= .2
解：过D点作DE⊥x轴，垂足为E，
∵Rt△OAB中，∠OAB=90°，
∴DE∥AB，
∵D为Rt△OAB斜边OB的中点D，
∴DE为Rt△OAB的中位线，
∵△OED∽△OAB，
∴两三角形的相似比为
,
∵双曲线，可知
，
，
由
，
得
，
解得
∵Rt△OAB中，∠OAB=90°，
∴DE∥AB，
∵D为Rt△OAB斜边OB的中点D，
∴DE为Rt△OAB的中位线，
∵△OED∽△OAB，
∴两三角形的相似比为
,∵双曲线
，可知，，由
，得
，解得
练习册系列答案
名校课堂系列答案
相关题目
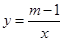的图象如图，则m的取值范围是 ．
，恰好经过BC的中点D，则K的值为_______________.
图象上有三个点
，
，
，其中
，则
，
，
的大小关系是（ ）
B．
C．
D．
图象上一点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交反比例函数
图象于E、F两点． 用含k1、k2的式子表示四边形PEOF的面积为 ；
的图象经过点
，则a的值为 ．