题目内容
(2008•朝阳区一模)我们给出如下定义:若一个四边形中存在一组对边的平方和等于另一组对边的平方和,则称这个四边形为等平方和四边形,
(1)写出一个你所学过的特殊四边形中是等平方和四边形的图形的名称:
(2)如图(1),在梯形ABCD中,AD∥BC,AC⊥BD,垂足为O.求证:AD2+BC2=AB2+DC2,即四边形ABCD是等平方和四边形.

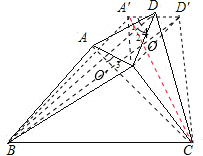
(3)如果将图(1)中的△AOD绕点O按逆时针方向旋转α度(0<α<90)后得到图(2),那么四边形ABCD能否成为等平方和四边形?若能,请你证明;若不能,请说明理由.
(1)写出一个你所学过的特殊四边形中是等平方和四边形的图形的名称:
菱形或正方形
菱形或正方形
,(2)如图(1),在梯形ABCD中,AD∥BC,AC⊥BD,垂足为O.求证:AD2+BC2=AB2+DC2,即四边形ABCD是等平方和四边形.

(3)如果将图(1)中的△AOD绕点O按逆时针方向旋转α度(0<α<90)后得到图(2),那么四边形ABCD能否成为等平方和四边形?若能,请你证明;若不能,请说明理由.
分析:(1)据题中定义,只要邻边相等的平行四边形即符合要求,则菱形或正方形都符合要求.
(2)根据AC⊥BD和勾股定理易证得AD2+BC2=AB2+DC2即四边形ABCD是等平方和四边形.
(3)作出原梯形A′BCD′,连接AC、BD交于O′,首先证明A′OD′∽△COB,再证明△AOC∽△DOB,可得∠AOD=∠AOD=90°,以下同(2)的证法即得到AD2+BC2=AB2+DC2即四边形ABCD是等平方和四边形.
(2)根据AC⊥BD和勾股定理易证得AD2+BC2=AB2+DC2即四边形ABCD是等平方和四边形.
(3)作出原梯形A′BCD′,连接AC、BD交于O′,首先证明A′OD′∽△COB,再证明△AOC∽△DOB,可得∠AOD=∠AOD=90°,以下同(2)的证法即得到AD2+BC2=AB2+DC2即四边形ABCD是等平方和四边形.
解答:解:(1)菱形或正方形;(1分)
(2)证明:∵AC⊥BD,
∴∠AOD=∠BOC=∠AOB=∠DOC=90°
∴OA2+OD2=AD2;OB2+OC2=BC2;OA2+OB2=AB2;OD2+OC2=DC2.
∴AD2+BC2=AB2+DC2即四边形ABCD是等平方和四边形.(3分)
(3)解:四边形ABCD是等平方和四边形.
证明:原梯形记为A′BCD′,
依题意旋转后得四边形ABCD,连接AC、BD交于点O′,
∵A′D′∥BC,
∴A′OD′∽△COB,
∴
=
,
∵OA′=OA,OD′=OD,
∴
=
,
∵∠AOA'=∠DOD'=α,
∴∠AOC=∠DOB=180°-α,
又∵
=
,
∴△AOC∽△DOB;(5分)
∴∠1=∠2
又∵∠3=∠4,
∴∠AO′D=∠AOD=90°,
由(2)的结论得:AD2+BC2=AB2+DC2.
即四边形ABCD是等平方和四边形.(7分)
(2)证明:∵AC⊥BD,
∴∠AOD=∠BOC=∠AOB=∠DOC=90°
∴OA2+OD2=AD2;OB2+OC2=BC2;OA2+OB2=AB2;OD2+OC2=DC2.
∴AD2+BC2=AB2+DC2即四边形ABCD是等平方和四边形.(3分)
(3)解:四边形ABCD是等平方和四边形.
证明:原梯形记为A′BCD′,
依题意旋转后得四边形ABCD,连接AC、BD交于点O′,

∵A′D′∥BC,
∴A′OD′∽△COB,
∴
| OA′ |
| OC |
| OD′ |
| OB |
∵OA′=OA,OD′=OD,
∴
| OA |
| OC |
| OD |
| OB |
∵∠AOA'=∠DOD'=α,
∴∠AOC=∠DOB=180°-α,
又∵
| OA |
| OC |
| OD |
| OB |
∴△AOC∽△DOB;(5分)
∴∠1=∠2
又∵∠3=∠4,
∴∠AO′D=∠AOD=90°,
由(2)的结论得:AD2+BC2=AB2+DC2.
即四边形ABCD是等平方和四边形.(7分)
点评:本题考查学生对一个新的定义的理解,涉及到相似三角形的判定及性质、勾股定理的、菱形、正方形的性质等知识点,是一道考查学生综合能力的好题.

练习册系列答案
相关题目
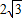 ,点E在AB的延长线上,且
,点E在AB的延长线上,且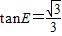 .
.