题目内容
若在Rt△ABC中,∠C=90°,AC=2 ,BC=2,则∠A=________°.
,BC=2,则∠A=________°.
30
分析:根据勾股定理,求出斜边的长度后,再根据锐角三角函数的定义求出∠A.
解答: 解:在Rt△ABC中,
解:在Rt△ABC中,
∵∠C=90°,AC=2 ,BC=2,
,BC=2,
∴tanA= =
= =
= ,
,
∴∠A=30°.
故答案为:30.
点评:此题主要考查了勾股定理、锐角三角函数的定义,解题的关键在于求出斜边的长度,然后根据正切的定义即可求出结果.
分析:根据勾股定理,求出斜边的长度后,再根据锐角三角函数的定义求出∠A.
解答:
 解:在Rt△ABC中,
解:在Rt△ABC中,∵∠C=90°,AC=2
 ,BC=2,
,BC=2,∴tanA=
 =
= =
= ,
,∴∠A=30°.
故答案为:30.
点评:此题主要考查了勾股定理、锐角三角函数的定义,解题的关键在于求出斜边的长度,然后根据正切的定义即可求出结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
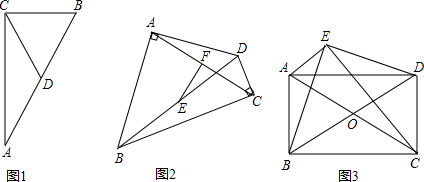
 (1)如图,若在△ABC中有三个内接正方形,其边长分别为a=7,b=5,c=2.试证明∠ACB为直角.
(1)如图,若在△ABC中有三个内接正方形,其边长分别为a=7,b=5,c=2.试证明∠ACB为直角.
 ,你能用矩形的性质说明这个结论吗?请说明.
,你能用矩形的性质说明这个结论吗?请说明. ,BC=2,则∠A= °.
,BC=2,则∠A= °.