题目内容
 27、如图,已知AB∥DE,AC∥DF.
27、如图,已知AB∥DE,AC∥DF.(1)试说明:∠A=∠D;
(2)把上面的结论仿照“两直线平行,同位角相等”的形式用文字写出来;
(3)在这个条件下,∠A和∠D还有其他关系吗?如果你认为有,请写出来,不需说明理由.
分析:图中有平行线,却无直线同时截AB、AC、DE、DF,所以暂时无法运用平行线的性质转化.若延长DE交AC于O,构造平行线的截线,则根据平行线的性质容易证明.
解答: (1)如图,设DE与AC交于点O,
(1)如图,设DE与AC交于点O,
∵AB∥DE,
∴∠A=∠POC(两直线平行,同位角相等).
∵AC∥DF,
∴∠D=∠POC(两直线平行,同位角相等).
∴∠A=∠D.
(2)一个角的两边与另一个角的两边分别平行,那么这两个角相等.(意思相近即可得分)
(3)∠A与∠D互补.
 (1)如图,设DE与AC交于点O,
(1)如图,设DE与AC交于点O,∵AB∥DE,
∴∠A=∠POC(两直线平行,同位角相等).
∵AC∥DF,
∴∠D=∠POC(两直线平行,同位角相等).
∴∠A=∠D.
(2)一个角的两边与另一个角的两边分别平行,那么这两个角相等.(意思相近即可得分)
(3)∠A与∠D互补.
点评:解答此类题,若平行线无截线,可适当构造截线转化角的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 5、如图,已知AB∥DE,∠A=136°,∠C=164°,则∠D的度数为( )
5、如图,已知AB∥DE,∠A=136°,∠C=164°,则∠D的度数为( ) 如图,已知AB=DE,BC=EF,∠B=∠E,A、F、C、D在同一条直线上,
如图,已知AB=DE,BC=EF,∠B=∠E,A、F、C、D在同一条直线上, 如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
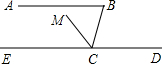 如图,已知AB∥DE,∠B=80°,CM平分∠BCE,求∠DCM的度数.
如图,已知AB∥DE,∠B=80°,CM平分∠BCE,求∠DCM的度数.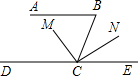 如图,已知AB∥DE,∠B=80°,CM平分∠BCD,CM⊥CN,垂足为C.求∠NCE的度数.
如图,已知AB∥DE,∠B=80°,CM平分∠BCD,CM⊥CN,垂足为C.求∠NCE的度数.