题目内容
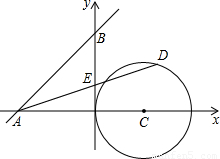
如图,直线 分别与两坐标轴交于A,B两点,点C从A点出发沿射线BA方向移动,速度为每秒1个单位长度.以C为顶点作等边△CDE,其中点D和点E都在x轴上.半径为
分别与两坐标轴交于A,B两点,点C从A点出发沿射线BA方向移动,速度为每秒1个单位长度.以C为顶点作等边△CDE,其中点D和点E都在x轴上.半径为 的⊙M与x轴、直线AB相切于点G、F.
的⊙M与x轴、直线AB相切于点G、F.

(1)直线AB与x轴所夹的角∠ABO= °;
(2)求当点C移动多少秒时,等边△CDE的边CE与⊙M相切?
【答案】
(1)30;(2)4或 .
.
【解析】
试题分析:(1)根据直线解析式求出OA、OB的长度,再由∠ABO的正切值,可求出∠AOB的度数:直线AB的解析式为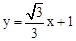 ,令x=0,则y=1,令y=0,则
,令x=0,则y=1,令y=0,则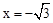 ,∵
,∵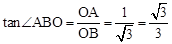 ,∴∠ABO=30°;(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
,∴∠ABO=30°;(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
试题解析:(1)30;
(2)设点C移动t秒后与⊙M相切,
①当CE在⊙M左侧相切于点H,如图(1),连接MF、MG、MH,
∵AB、CE、BO均为⊙M的切线,∴MF⊥AB,MH⊥CE,MG⊥BO.
∵∠ABO=30°,△CDE是等边三角形,∴∠BCE=90°. ∴四边形CHMF为矩形.
∵MF=MH,∴四边形CHMF为正方形. ∴CH=MH=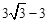 .
.
∵EH、EG为⊙M的切线,∠CED=60°,∴∠HEM=60°. ∴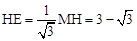 .
.
∵ ,∴
,∴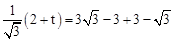 ,解得t=4.
,解得t=4.

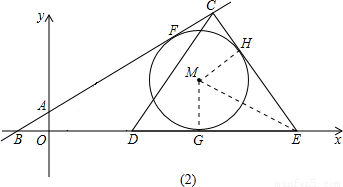
②当CE在⊙M右侧相切于点H(如图(2)),
由①证得:CH=MH=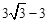 .
.
∵∠HEM=30°,∴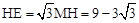 .
.
∴ ,解得,t=
,解得,t= .
.
考点:1.圆的综合题;2.动点问题;3.锐角三角函数定义;4.特殊角的三角函数值;5.切线的性质;6. 等边三角形的性质;7. 正方形的判定和性质;8.分类思想的应用.

练习册系列答案
相关题目

 (2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是
(2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是
 如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是________.
如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是________.