题目内容
 阅读并填空:
阅读并填空:
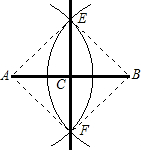
如图:根据六年级第二学期学过的用直尺、圆规作线段中点的方法,画出了线段AB的中点C,请说明这种方法正确的理由.
解:连接AE、BE、AF、BF.
在△AEF和△BEF中,
EF=EF(________),
________=________(画弧时所取的半径相等),
________=________(画弧时所取的半径相等).
所以△AEF≌△BEF (________).
所以∠AEF=∠BEF (________).
又AE=BE,
所以AC=BC (________).
即点C是线段AB的中点.
公共边 AE BE AF BF SSS 全等三角形的对应角相等 等腰三角形三线合一
分析:根据SSS证△AEF≌△BEF,推出∠AEF=∠BEF,根据等腰三角形性质求出即可.
解答:在△AEF和△BEF中,
 ,
,
∴△AEF≌△BEF(SSS),
∴∠AEF=∠BEF(全等三角形的对应角相等),
∵AE=BE,
∴AC=BC(等腰三角形的三线合一),
∴C是线段AB的中点.
故答案为:公共边,AE、BE,AF、BF,S.S.S,全等三角形对应角相等,等腰三角形三线合一.
点评:本题主要考查对等腰三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,能推出∠AEF=∠BEF是解此题的关键.
分析:根据SSS证△AEF≌△BEF,推出∠AEF=∠BEF,根据等腰三角形性质求出即可.
解答:在△AEF和△BEF中,
 ,
,∴△AEF≌△BEF(SSS),
∴∠AEF=∠BEF(全等三角形的对应角相等),
∵AE=BE,
∴AC=BC(等腰三角形的三线合一),
∴C是线段AB的中点.
故答案为:公共边,AE、BE,AF、BF,S.S.S,全等三角形对应角相等,等腰三角形三线合一.
点评:本题主要考查对等腰三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,能推出∠AEF=∠BEF是解此题的关键.

练习册系列答案
相关题目
 21、阅读并解答
21、阅读并解答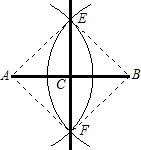 阅读并填空:
阅读并填空: