题目内容
一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k＜0；②a＞0；③当x＜4时，y1＜y2中，正确的个数是（ ）分析：根据y1=kx+b和y2=x+a的图象可知：k＜0，a＜0，所以当x＜4时，相应的x的值，y1图象均高于y2的图象．
解答：解：根据图象y1=kx+b经过第一、二、四象限，
∴k＜0，
故①正确；
∵y2=x+a与y轴负半轴相交，
∴a＜0，
故②错误；
当x＜4时图象y1在y2的上方，应为当x＜4时y1＞y2，故③错误．
所以正确的有①共1个．
故选B．
∴k＜0，
故①正确；
∵y2=x+a与y轴负半轴相交，
∴a＜0，
故②错误；
当x＜4时图象y1在y2的上方，应为当x＜4时y1＞y2，故③错误．
所以正确的有①共1个．
故选B．
点评：此题主要考查了一次函数，以及一次函数与不等式，根据函数图象的走势和与y轴的交点来判断各个函数k，b的值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14、一次函数y1=kx+b与y2=x+a的图象如图所示，则下列结论：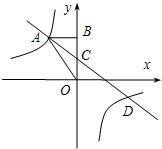
如图，已知一次函数y1=kx+b（k≠0）与反比例函数
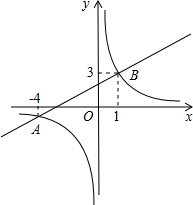，3）两点．
如图，A（-3，n）、B（2，-3）是一次函数y1=kx+b的图象和反比例函数y2=
如图，已知一次函数y1=kx+b的图象与反比例函数y2=