题目内容
如图,在▱ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为__________.

10.
【考点】相似三角形的判定与性质;平行四边形的性质.
【分析】根据平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似,再根据相似三角形的对应边成比例可解得AB的长,而在▱ABCD中,CD=AB.
【解答】解:∵EF∥AB
∴△DEF∽△DAB
∴EF:AB=DE:DA=DE:(DE+EA)=2:5
∴AB=10
∵在▱ABCD中AB=CD.
∴CD=10.
【点评】本题考查了相似三角形的判定和相似三角形的性质,以及平行四边形的性质,注意对应边的比不要搞错.

练习册系列答案
相关题目


 B.
B. C.
C. D.
D.
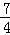 )2=
)2=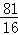 D.3x2﹣4x﹣2=0化为(x﹣
D.3x2﹣4x﹣2=0化为(x﹣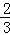 )2=
)2=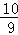
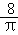 cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是__________.
cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是__________.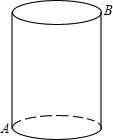
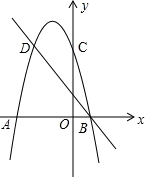
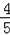
 ,则线段CE的最大值为 .
,则线段CE的最大值为 .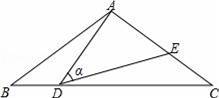

 C.10或2
C.10或2 D.无法确定
D.无法确定