题目内容
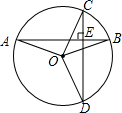 已知⊙O中,弦AB⊥弦CD于E,求证:∠AOD+∠BOC=180°.
已知⊙O中,弦AB⊥弦CD于E,求证:∠AOD+∠BOC=180°.
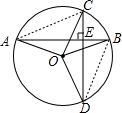 解:连接AC,BD,
解:连接AC,BD,由圆周角定理得:∠AOD=2∠ABD,∠BOC=2∠BOC,∠CAB=∠CBD
∵弦AB⊥弦CD
∴∠ABD+∠BDC=90°,
∴∠AOD+∠BOC=2∠ABD+2∠BOC=2(∠ABD+∠BDC)=2×90°=180°
分析:连接AC,BD,由圆周角定理得:∠AOD=2∠ABD,∠BOC=2∠BOC,∠CAB=∠CBD,然后利用垂直的定义求得∠ABD+∠BDC=90°,从而得证.
点评:本题考查了圆周角定理的知识,解题的关键是正确的作出辅助线构造同弧所对的圆心角和圆周角.

练习册系列答案
相关题目
 9、如图所示,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是( )
9、如图所示,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是( )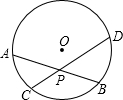 如图,已知⊙O中,弦AB与CD相交于点P.
如图,已知⊙O中,弦AB与CD相交于点P.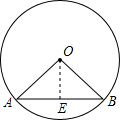 如图,已知⊙O中,弦AB=12cm,O点到AB的距离等于AB的一半,则∠AOB的度数为
如图,已知⊙O中,弦AB=12cm,O点到AB的距离等于AB的一半,则∠AOB的度数为