Question

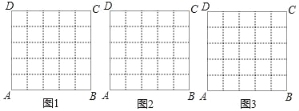
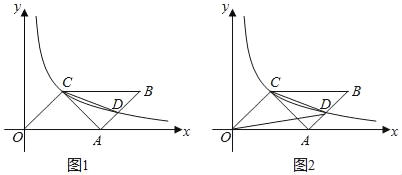
【题目】如图1，在平面直角坐标系中，OABC的一个顶点与坐标原点重合，OA边落在x轴上，且OA=4，OC=2，∠COA=45°．反比例函数y=（k＞0，x＞0）的图象经过点C，与AB交于点D，连接AC，CD．

（1）试求反比例函数的解析式；

（2）求证：CD平分∠ACB；

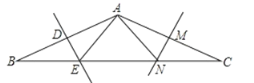
（3）如图2，连接OD，在反比例的函数图象上是否存在一点P，使得S△POC=S△COD？如果存在，请直接写出点P的坐标．如果不存在，请说明理由．

Answer 1

【答案】（1）；（2）证明见解析；（3） P的坐标为（﹣1， +1）或P（+1， ﹣1）．

【解析】试题分析：（1）过点C作CE⊥x轴于E，已知OC=2，∠COA=45°，根据勾股定理求得OE=CE=2，即可得点C的坐标，代入y=求得k值，即可得反比例函数的解析式；（2）过点D作DG⊥x轴于G，交BC于F，先求得直线AB的解析式，把反比例函数的解析式和直线AB的解析式联立，解方程组，求得点D的坐标，再求得AD和DE的长，根据角平分线的判定定理即可证得CD平分∠ACB；（3）存在，分点P在点C右侧时和点P在点C左侧时两种情况求点P的坐标即可.

试题解析：

（1）如图1，过点C作CE⊥x轴于E，

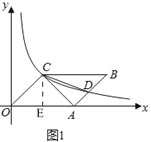
∴∠CEO=90°，

∵∠COA=45°，

∴∠OCE=45°，

∵OC=2，

∴OE=CE=2，

∴C（2，2），

∵点C在反比例函数图象上，

∴k=2×2=4，

∴反比例函数解析式为y=，

（2）如图2，过点D作DG⊥x轴于G，交BC于F，

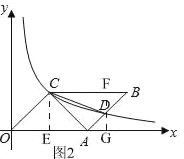
∵CB∥x轴，

∴GF⊥CB，

∵OA=4，

由（1）知，OC=CE=2，

∴AE=EC=2，

∴∠ECA=45°，∠OCA=90°，

∵OC∥AB，

∴∠BAC=∠OCA=90°，

∴AD⊥AC，

∵A（4，0），AB∥OC，

∴直线AB的解析式为y=x﹣4①，

∵反比例函数解析式为y=②，

联立①②解得，或（舍），

∴D（2+2，2﹣2），

∴AG=DG=2﹣2，

∴AD=DG=4﹣2，

∴DF=2﹣（2﹣2）=4﹣2，

∴AD=DF，

∵AD⊥AC，DF⊥CB，

∴点D是∠ACB的角平分线上，

即：CD平分∠ACB；

（3）存在，∵点C（2，2），

∴直线OC的解析式为y=x，OC=2，

∵D（2+2，2﹣2），

∴CD=2﹣2

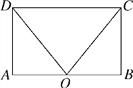
Ⅰ、如图3，当点P在点C右侧时，即：点P的横坐标大于2，

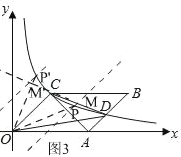
∵S△POC=S△COD，

∴设CD的中点为M，

∴M（+2，），

过点M作MP∥OC交双曲线于P，

∴直线PM的解析式为y=x﹣2③，

∵反比例函数解析式为y=④，

联立③④解得，

或（舍），

∴P（+1，﹣1）；

Ⅱ、当点P'在点C左侧时，即：点P'的横坐标大于0而小于2，

设点M关于OC的对称点为M'，M'（m，n），

∴=2， =2，

∴m=2﹣，n=4﹣，

∴M'（2﹣，4﹣），

∵P'M'∥OC，

∴直线P'M'的解析式为y=x+2⑤，

联立④⑤解得，或（舍），

∴P'（﹣1， +1）．

即：点P的坐标为（﹣1， +1）或P（+1，﹣1）．