题目内容
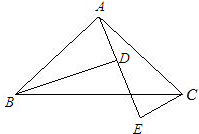
 已知如图,AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB的值为
已知如图,AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB的值为
- A.2
- B.3
- C.4
- D.5
C
分析:根据相似三角形的判定及已知可得到△ABC∽△CDE,利用相似三角形的对应边成比例即可求得AB的长.
解答:∵C是线段BD的中点,BD=4,
∴BC=CD=2,
∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°,∠A+∠ACB=90°,
∵AC⊥CE,即∠ECD+∠ACB=90°,
∴∠A=∠ECD,
∴△ABC∽△CDE,
∴ =
= ,
,
∴ =
= ,
,
∴AB=4,
故选C.
点评:本题主要考查相似三角形的判定、相似三角形的性质等知识,关键是推出△ABC∽△CDE.
分析:根据相似三角形的判定及已知可得到△ABC∽△CDE,利用相似三角形的对应边成比例即可求得AB的长.
解答:∵C是线段BD的中点,BD=4,
∴BC=CD=2,
∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°,∠A+∠ACB=90°,
∵AC⊥CE,即∠ECD+∠ACB=90°,
∴∠A=∠ECD,
∴△ABC∽△CDE,
∴
 =
= ,
,∴
 =
= ,
,∴AB=4,
故选C.
点评:本题主要考查相似三角形的判定、相似三角形的性质等知识,关键是推出△ABC∽△CDE.

练习册系列答案
相关题目
 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E. 已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)
已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)
