��Ŀ����
��ͼ����֪��O��Բ��������ԭ�㣬�뾶Ϊ2����Բ��һ��T��| 2 |
| 2 |
��1����OA��OB�ij���
��2��������AB��ȡһ��C����CΪԲ�ģ��뾶Ϊr�ġ�C���O������P�㣬��Բ���ڹ�����PM��OT���ӳ�����M����M������C������MN���е�ΪN����֤��MN=TC��MN��TC��
��3������2���еġ�C��Բ����AB���ƶ���ʼ�����O���У���r�ڱ仯����N������
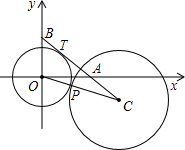 Ϊ��x��y������N�������x��y�ܷ�д����r�صĹ�ϵʽ�����ܣ���д����ϵʽ�������ܣ���˵�����ɣ�
Ϊ��x��y������N�������x��y�ܷ�д����r�صĹ�ϵʽ�����ܣ���д����ϵʽ�������ܣ���˵�����ɣ�
��������1�����ݵ�T������֪����TOA=45�㣬����BA�С�O��T����OT��BA���ʡ�OAB=��OBA=45�㣬��T��TG��x����G����TG=OG=GA=
���ɴ˿����OA��OB�ij���
��2������PM����Բ�Ĺ����ߣ���MP��OC����OP��OT���ǡ�O�İ뾶����֤��Rt��MOP��Rt��COT����MP=TC�������߳�����֪MP=MN�����ɵõ�TC=MN��������ȫ�������λ��ɵ�OM=OC��������Բ�İ뾶�ͣ���MT=CN����֪��MTC=��MNC=90�㣬����֤��MN��TC��������MC��ͨ��֤������ȫ�ȵ�MN��TC���ڴ�����ȣ���
��3����MN��x��Ľ���ΪD����N��NH��x����H���ɣ�2��MN��TC֪��TMN=90�㣬���MOD����HND���ǵ���ֱ�������Σ���ôOD=OH+HN=x+y����OD=
OM��OM������Բ�İ뾶�ͣ�����������ʽ�ɵ�x��y��r�ĵ�һ����ϵʽ�������MN�ij�����TC�ij�������Rt��OTC�У����ݹ��ɶ����õ�����һ��x��y��r�Ĺ�ϵʽ��������ʽ���ɵõ�x��y�Ĺ�ϵʽ��
| 2 |
��2������PM����Բ�Ĺ����ߣ���MP��OC����OP��OT���ǡ�O�İ뾶����֤��Rt��MOP��Rt��COT����MP=TC�������߳�����֪MP=MN�����ɵõ�TC=MN��������ȫ�������λ��ɵ�OM=OC��������Բ�İ뾶�ͣ���MT=CN����֪��MTC=��MNC=90�㣬����֤��MN��TC��������MC��ͨ��֤������ȫ�ȵ�MN��TC���ڴ�����ȣ���
��3����MN��x��Ľ���ΪD����N��NH��x����H���ɣ�2��MN��TC֪��TMN=90�㣬���MOD����HND���ǵ���ֱ�������Σ���ôOD=OH+HN=x+y����OD=
| 2 |
��� ��1���⣺��T��TG��x����G��
��1���⣺��T��TG��x����G��
��T�����꣨
��
����
��OG=GT=
��
���TOG=45�㣬
���OAB=45�㣬
����AOB�ǵ���ֱ�������Σ�
��OA=OB=
OT=2
��
��2��֤������PM����Բ���ڹ����ߣ�
��MP��OC��
��Rt��MOP��Rt��COT��
��MP=CT��
��MN��MP�ǡ�C�����߳���
��MP=MN��
��MN=TC �٣�
�����ϣ���OC=MO��
��r+2=MT+2��MT=r��
��CN=r��
��MT=NC��
�ߡ�MNC=��MTC=90�㣬
��MN��TC�ڣ�
��MN=TC��
��3���⣺��д����r�ص�ʽ�ӣ���ֱ��MN��x����D����N��NH��x����H��
�ɣ�1������2����֪����OMD����NHD���ǵ���ֱ�������Σ�
��OD=OH+HD=OH+HN=x+y����OD=x+y��
��OD=
OM=
��2+r����
��x+y=
(2+r)�٣�
MN=MD-ND=OM-ND=��2+r��-
y��
��MN=��2+r��-
y��
��Rt��OTC��
��OT2+TC2=OC2����TC=MN��
��22+[��2+r��-
y]2=��2+r��2�ڣ�
�ɢ٣���2+r=
(x+y)������ڵã�4+[
(x+y)-
y]2=��
��2��
���xy=2��y=
��
 ��1���⣺��T��TG��x����G��
��1���⣺��T��TG��x����G����T�����꣨
| 2 |
| 2 |
��OG=GT=
| 2 |
���TOG=45�㣬
���OAB=45�㣬
����AOB�ǵ���ֱ�������Σ�
��OA=OB=
| 2 |
| 2 |
��2��֤������PM����Բ���ڹ����ߣ�
��MP��OC��
��Rt��MOP��Rt��COT��
��MP=CT��
��MN��MP�ǡ�C�����߳���
��MP=MN��
��MN=TC �٣�
�����ϣ���OC=MO��

��r+2=MT+2��MT=r��
��CN=r��
��MT=NC��
�ߡ�MNC=��MTC=90�㣬
��MN��TC�ڣ�
��MN=TC��
��3���⣺��д����r�ص�ʽ�ӣ���ֱ��MN��x����D����N��NH��x����H��
�ɣ�1������2����֪����OMD����NHD���ǵ���ֱ�������Σ�
��OD=OH+HD=OH+HN=x+y����OD=x+y��
��OD=
| 2 |
| 2 |
��x+y=
| 2 |
MN=MD-ND=OM-ND=��2+r��-
| 2 |
��MN=��2+r��-
| 2 |
��Rt��OTC��
��OT2+TC2=OC2����TC=MN��
��22+[��2+r��-
| 2 |
�ɢ٣���2+r=
| 1 | ||
|
| 1 | ||
|
| 2 |
| x+y | ||
|
���xy=2��y=
| 2 |
| x |
���������⿼����������Բ�����ʡ����ߵ����ʡ����߳�������ȫ�������ε��ж������ʡ����ɶ�����Ӧ�õȣ��ۺ���ǿ���ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
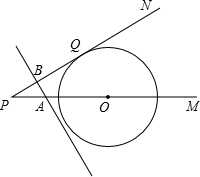 ����������ţ�
����������ţ�

 ��
�� �������߽�x����A�㣬��y����B�㣮
�������߽�x����A�㣬��y����B�㣮