Question

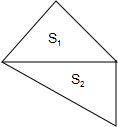将一副角板如图放置，则上、下两块三角板的面积S₁：S₂=

3

：2

．

Answer 1

分析：首先设两个三角板重合的边CA=x，再根据三角函数定义表示出AB、BC、CD的长，再利用三角形的面积公式表示出S₁、S₂，即可求出比值．

解答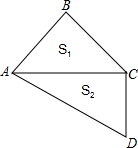：解：设两个三角板重合的边CA=x，
∵∠B=90°，∠BAC=∠ACB=45°，
∴CB=AB=CB•sin45°=

2

2

x，
∴S₁=

1

2

AB•CB=

1

2

×

2

2

x•

2

2

x=

1

4

x²，
在直角△ACD中：
∵∠CAD=30°，∠D=60°，
∴CD=AC•tan30°=

3

3

x，
∴S₂=

1

2

•AC•CD=

1

2

•x•

3

3

x=

3

6

x²，
∴S₁：S₂=

1

4

x²：

3

6

x²=

3

：2，
故答案为：

3

：2．

点评：此题主要考查了三角函数的应用，以及三角形的面积公式，题目难度不大，有利于锻炼学生综合运用所学知识的能力．解题时要注意认识图形，要注意方程思想的应用．