��Ŀ����
��֪����ͼ����ƽ��ֱ������ϵ�ڣ�Rt��ABC��б��AB��x���ϣ���C������Ϊ��0��6����AB=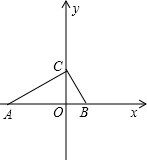 15����CBA����CAB����tan��CAB��tan��CBA�ǹ���x�ķ���x2+mx+n=0��������
15����CBA����CAB����tan��CAB��tan��CBA�ǹ���x�ķ���x2+mx+n=0����������1����m��n��ֵ��
��2������ACB�Ľ�ƽ���߽�x����D����ֱ��CD�Ľ���ʽ��
��3���ڣ�2���������£�ֱ��CD���Ƿ���ڵ�M����M����BC��ƽ���ߣ���y����N��ʹ��M��N��B��CΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д��M������ꣻ�������ڣ���˵�����ɣ�
��������1�������⣬��֪OC=6��AB=15����ֱ�������ε�ͼ���ϵ���ɵã�OC2=OA•OB��OB=AB-OA���ⷽ�̿ɵ�OA��OB��ֵ��tan��CAB��tan��CBA�����֡�CBA����CAB����tan��CAB��tan��CBA�ǹ���x�ķ���x2+mx+n=0����������m��n����
��2����D��DE��AC������ΪE��
��Ϊ��ACB�Ľ�ƽ���߽�x����D�����ԡ�DCE=��EDC=45�㣬CE=DE����OA=12��OB=3����AC=6
��BC=3
����DE=CE=y����
=
����AD=
�٣���CD=
y��AE=AC-CE=6
-y���ɵ�AD=
=
�ڣ��ɢ٢ڿɵã�y=2
����AD=10����OD=2����D������Ϊ��-2��0�����Ӷ�ֱ��CD�Ľ���ʽ����
��3�����ڣ�M1��3��15����M2��-3��-3����
��2����D��DE��AC������ΪE��
��Ϊ��ACB�Ľ�ƽ���߽�x����D�����ԡ�DCE=��EDC=45�㣬CE=DE����OA=12��OB=3����AC=6
| 5 |
| 5 |
| AD |
| AB |
| DE |
| BC |
| 15y | ||
3
|
| 2 |
| 5 |
| AE2+DE2 |
y2+(6
|
| 5 |
��3�����ڣ�M1��3��15����M2��-3��-3����
��� �⣺��1���ߡ�B+��A=90�㣬��B+��BCO=90�㣬
�⣺��1���ߡ�B+��A=90�㣬��B+��BCO=90�㣬
���A=��BCO����AOC=��COB=90�㣬
���AOC�ס�COB
��
=
��
��OC2=OA•OB��
�֡�OB=AB-OA��
��
=
�����OA=12��3���ɡ�CBA����CAB
��OA=12��OB=3��
��tan��CAB=
��tan��CBD=2��
��tan��CAB��tan��CBA�ǹ���x�ķ���x2+mx+n=0��������
��
+
m+n=0�٣�4+2m+n=0�ڣ�
��٢���ɵķ����飬�ã�m=-
��n=1��
��2����D����DE��AC������ΪE��
�ߡ�ACB�Ľ�ƽ���߽�x����D��
���DCE=��EDC=45�㣬CE=DE��
��OA=12��OB=3��
��AC=6
��BC=3
����DE=CE=y��
��
=
��
��AD=
�٣���CD=
y��AE=AC-CE=6
-y��
��AD=
=
�ڣ�
�ɢ٢ڿɵã�y=2
��
��AD=10��
��OD=2��
��D��������-2��0����
��ֱ��CD�Ľ���ʽΪy=kx+b����C��0��6����D��-2��0�������ã�k=3��b=6��
��y=3x+6��
��3�����ڣ�M1��3��15����M2��-3��-3��
 �⣺��1���ߡ�B+��A=90�㣬��B+��BCO=90�㣬
�⣺��1���ߡ�B+��A=90�㣬��B+��BCO=90�㣬���A=��BCO����AOC=��COB=90�㣬
���AOC�ס�COB
��
| OC |
| OA |
| OB |
| OC |
��OC2=OA•OB��
�֡�OB=AB-OA��
��
| 6 |
| OA |
| 15-OA |
| 6 |
��OA=12��OB=3��
��tan��CAB=
| 1 |
| 2 |
��tan��CAB��tan��CBA�ǹ���x�ķ���x2+mx+n=0��������
��
| 1 |
| 4 |
| 1 |
| 2 |
��٢���ɵķ����飬�ã�m=-
| 5 |
| 2 |
��2����D����DE��AC������ΪE��
�ߡ�ACB�Ľ�ƽ���߽�x����D��
���DCE=��EDC=45�㣬CE=DE��
��OA=12��OB=3��
��AC=6
| 5 |
| 5 |
��
| AD |
| AB |
| DE |
| BC |
��AD=
| 15y | ||
3
|
| 2 |
| 5 |
��AD=
| AE2+DE2 |
y2+(6
|
�ɢ٢ڿɵã�y=2
| 5 |
��AD=10��
��OD=2��
��D��������-2��0����
��ֱ��CD�Ľ���ʽΪy=kx+b����C��0��6����D��-2��0�������ã�k=3��b=6��
��y=3x+6��
��3�����ڣ�M1��3��15����M2��-3��-3��
�����������Ǵ����뼸�����ϵ��ۺϿ����⣬���õ���֪ʶ��㣬�ѶȽϴ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ
��ͼ����ƽ��ֱ������ϵ�У�ֱ ��ͼ����ƽ��ֱ������ϵ�У�ԭ��O����һƹ������������з���ƹ����ƹ�������·����һ�������ߣ��ڵ������������X����Ϊ��B���������߶�OB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ��ǵ�Բ����Ͱ����ͼ��ƹ��������Ͱ�ڣ���֪OB=4�ף�OC=3�ף�ƹ����������߶�MN=5�ף�Բ����Ͱ��ֱ��Ϊ0.5����Ϊ0.3�ף�ƹ����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ���
��ͼ����ƽ��ֱ������ϵ�У�ԭ��O����һƹ������������з���ƹ����ƹ�������·����һ�������ߣ��ڵ������������X����Ϊ��B���������߶�OB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ��ǵ�Բ����Ͱ����ͼ��ƹ��������Ͱ�ڣ���֪OB=4�ף�OC=3�ף�ƹ����������߶�MN=5�ף�Բ����Ͱ��ֱ��Ϊ0.5����Ϊ0.3�ף�ƹ����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ���

