题目内容
 如图,Rt△AOB中∠AOB=90°,点A在y=-
如图,Rt△AOB中∠AOB=90°,点A在y=- 上,点B在y=
上,点B在y= 上,则
上,则 =________.
=________.

分析:作AC⊥x轴于C,作BD⊥x轴于D,易证△AOC∽△OBD,根据相似三角形的对应边的比相等,可以设
 =
= =
= =k,设A的坐标是(m,n),B的坐标是(p,q),则AC=n,OC=-m,BD=q,OD=p,即可求得k的值.
=k,设A的坐标是(m,n),B的坐标是(p,q),则AC=n,OC=-m,BD=q,OD=p,即可求得k的值.解答:
 解:作AC⊥x轴于C,作BD⊥x轴于D.则∠ACO=∠ODB=90°,
解:作AC⊥x轴于C,作BD⊥x轴于D.则∠ACO=∠ODB=90°,∵∠AOC=90°,
∴∠AOC+∠BOD=90°,
又∵直角△AOC中,∠AOC+∠CAO=90°,
∴∠CAO=∠DOB
∴△AOC∽△OBD,
∴设
 =
= =
= =k,
=k,设A的坐标是(m,n),B的坐标是(p,q),则AC=n,OC=-m,BD=q,OD=p,
∴
 =
= =k,则m=-qk,n=pk,
=k,则m=-qk,n=pk,∵(m,n)在函数y=-
 上,即mn=-4,同理,pq=6,
上,即mn=-4,同理,pq=6,∴-pq•k2=-4,
∴k2=
 ,
,∴k=
 或-
或- (舍去).
(舍去).故
 =
= .
.故答案是:
 .
.点评:本题是相似三角形的性质和反比例函数的综合应用,证得△AOC∽△OBD,把所求的两线段的长的比值转化成两个三角形的相似比是关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
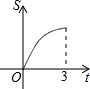
 如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )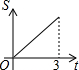


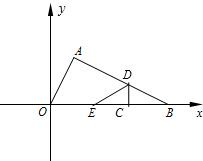 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程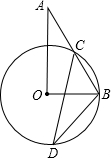 如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数.
如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数. 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程 如图,Rt△AOB中∠AOB=90°,点A在y=-
如图,Rt△AOB中∠AOB=90°,点A在y=-