Question

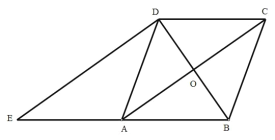
【题目】如图，在平行四边形ABCD中，F，G分别为CD，AD的中点，BF=2，BG=3，，则BC的长度为（ ）

A. B. C. 2.5D.

Answer 1

【答案】A

【解析】

延长AD、BF交于E,过点E作EM⊥BG，根据F是中点得到△CBF≌△DEF，得到BE=2BF=4，根据得到BM=BE=2，ME=2，故MG=1，再根据勾股定理求出EG的长，再得到DE的长即可求解.

延长AD、BF交于E,

∵F是中点，∴CF=DF,又AD∥BC，∴∠CBF=∠DEF，又∠CFB=∠DFE，

∴△CBF≌△DEF，∴BE=2BF=4，

过点E作EM⊥BG，∵，∴∠BEM=30°，

∴BM=BE=2，ME=2，

∴MG=BG-BM=1，

在Rt△EMG中，EG==

∵G为AD中点，∴DG=AD=DE，

∴DE==，

故BC=，

故选A.