Question

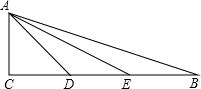如图，在RT△ABC中，∠C=90°，且AC=CD=1，又E，D为CB的三等分点．
（1）图中是否存在相似三角形，若存在，找出并证明相似的三角形；若不存在，试说明理由．
（2）比较∠ADC与∠AEC+∠B的大小，试说明理由．

Answer 1

分析：（1）存在，△ADE∽△BDA．∵AC=CD=DE=EB=1，∠C=90°，利用勾股定理易求AD=

2

，从而可求

DE

AD

=

1

2

=

2

2

；

DA

BD

=

2

2

，那么DE：AD=DA：BD，又∠ADE=∠BDA，那么可证△ADE∽△BDA；（2）
由于△ADE∽△BDA，利用形似三角形的性质可知∠DAE=∠B，再由三角形外角定义可知∠ADC=∠AEC+∠DAE，等量代换即可证明．

解答：解：（1）△ADE∽△BDA．
理由：∵AC=CD=DE=EB=1，
又∠C=90°，
∴AD=

2

，
∴

DE

AD

=

1

2

=

2

2

；

DA

BD

=

2

2

，
∴

DE

AD

=

DA

BD

，
又∵∠ADE=∠BDA，
∴△ADE∽△BDA；

（2）已证△ADE∽△BDA，
∴∠DAE=∠B，
又∵∠ADC=∠AEC+∠DAE，
∴∠ADC=∠AEC+∠B．

点评：本题考查了勾股定理、相似三角形的判定和性质、三角形外角定义，如果两个三角形两组对应边成比例，且夹角相等则两三角形相似．