Question

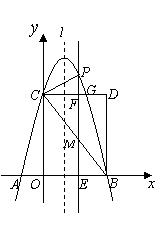
如图，平面直角坐标系中，抛物线交轴于A、B两点（点B在点A的右侧），交轴于点C，以OC、OB为两边作矩形OBDC，CD交抛物线于G．（1）求OC和OB的长；

（2）抛物线的对称轴在边OB（不包括O、B两点）上作平行移动，交轴于点E，交CD于点F，交BC于点M，交抛物线于点P．设OE ＝m，PM ＝h，求h与m的函数关系式，并求出PM的最大值；

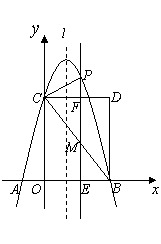
（3）连接PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△BEM相似？若存在，直接求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由．

Answer 1

解：（1）∵抛物线，

∴当=0时，=4；∴点C的坐标为（0，4）．  ∴OC=4   

∴当=0时，，解得．

∴点B的坐标为（3，0）      ∴OB=3．         

（2）∵抛物线的对称轴⊥轴，在边PE∥，∴PE⊥轴．

∵OE =m，∴点P的横坐标为m．               

∵点P在抛物线上，

∴点P的纵坐标为．                   

∴PE=．                               

在Rt△BOC中，tan∠OBC=．                     

在Rt△BME中，

ME=BE tan∠OBC=（OB－OE）·tan∠OBC=（3－m）=4－m．

∴PM = PE－ME =－4+m=．

∴ h与m的函数关系式为h=（0<m<3）   

又h=，

∵－<0，∴当m=时，h有最大值为3，∴PM的最大值为3．

（3）①当m=时，△PFC∽△BEM，此时△PCM为直角三角形

（∠PCM为直角）；                 

②当m=1时，△CFP∽△BEM，此时△PCM为等腰三角形（PC=CM）．