题目内容
直线l与两坐标轴的交点坐标分别是A（-3，0），B（0，4），0是坐标系原点，求直线l所对应的函数的表达式．
解：设直线l所对应的函数的表达式为：y=kx+b（k≠0）．
∵直线l与两坐标轴的交点坐标分别是A（-3，0），B（0，4），
∴A（-3，0），B（0，4）满足方程y=kx+b（k≠0），
∴
，
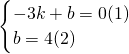解方程组得：
，
∴直线l所对应的函数的表达式为：y=
x+4．
分析：设直线l所对应的函数的表达式为：y=kx+b（k≠0），把满足该直线方程的点的坐标代入该方程，求出系数．
点评：用待定系数法确定函数的解析式，是常用的一种解题方法．
∵直线l与两坐标轴的交点坐标分别是A（-3，0），B（0，4），
∴A（-3，0），B（0，4）满足方程y=kx+b（k≠0），
∴
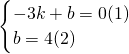，解方程组得：
，∴直线l所对应的函数的表达式为：y=
x+4．分析：设直线l所对应的函数的表达式为：y=kx+b（k≠0），把满足该直线方程的点的坐标代入该方程，求出系数．
点评：用待定系数法确定函数的解析式，是常用的一种解题方法．
练习册系列答案
相关题目
如图所示，直线L与两坐标轴的交点坐标分别是A（-3，0），B（0，4），O是坐标系原点．
如图，直线L与两坐标轴分别交于A、B点，且OA、OB的长是方程x2-14x+48=0的两根（OA＞OB），点C（-6，0）是x轴上一点，点P是直线L上一动点．
如图，直线L与两坐标轴分别交于A、B点，且OA、OB的长是方程x2-14x+48=0的两根（OA＞OB），点C（-6，0）是x轴上一点，点P是直线L上一动点．
如图所示，直线L与两坐标轴的交点坐标分别是A（-3，0），B（0，4），O是坐标系原点．