题目内容
 89、如图,在△AOB中,点C在OA上,点E,D在OB上,且CD∥AB,CE∥AD,AB=AD,试证明△CDE是等腰三角形.
89、如图,在△AOB中,点C在OA上,点E,D在OB上,且CD∥AB,CE∥AD,AB=AD,试证明△CDE是等腰三角形.分析:欲证△CDE是等腰三角形,又已知CD∥AB,CE∥AD,可利用三角形中两内角相等来证等腰.
解答:证明:∵CD∥AB,
∴∠CDE=∠B.
又∵CE∥AD,
∴∠CED=∠ADB.
又∵AB=AD,
∴∠B=∠ADB.
∴∠CDE=∠CED.
∴△CDE是等腰三角形.
∴∠CDE=∠B.
又∵CE∥AD,
∴∠CED=∠ADB.
又∵AB=AD,
∴∠B=∠ADB.
∴∠CDE=∠CED.
∴△CDE是等腰三角形.
点评:本题考查了等腰三角形的判定及平行线的性质;角的等量代换的运用是正确解答本题的关键.

练习册系列答案
相关题目
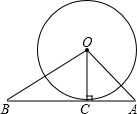 已知:如图,在△AOB中,OA⊥OB,OC⊥AB于C,OB=
已知:如图,在△AOB中,OA⊥OB,OC⊥AB于C,OB=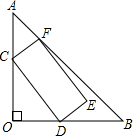 如图,在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上.
如图,在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上. 如图,在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上,若tanCDO=
如图,在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上,若tanCDO= 如图,在△AOB中,OA=OB,∠A=30°,⊙O经过AB的中点E分别交OA、OB于C、D两点,连接CD.
如图,在△AOB中,OA=OB,∠A=30°,⊙O经过AB的中点E分别交OA、OB于C、D两点,连接CD. 如图,在△AOB中,A、B两点的坐标分别为(2,4)和(6,2),求△AOB的面积.
如图,在△AOB中,A、B两点的坐标分别为(2,4)和(6,2),求△AOB的面积.