题目内容
【题目】如图,在平面直角坐标系中,![]() 的斜边
的斜边![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,且
,且![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.

(1)求反比例函数的表达式;
(2)若![]() 与
与![]() 关于直线
关于直线![]() 对称,一次函数
对称,一次函数![]() 的图象过点
的图象过点![]() ,求一次函数的表达式.
,求一次函数的表达式.
【答案】(1)y=![]() (2)y=
(2)y=![]() x﹣
x﹣![]()
【解析】
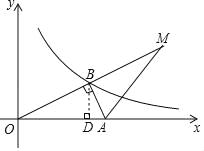
试题分析:(1)过点B作BD⊥OA于点D,设BD=a,通过解直角△OBD得到OD=2BD.然后利用勾股定理列出关于a的方程并解答即可;
(2)欲求直线AM的表达式,只需推知点A、M的坐标即可.通过解直角△AOB求得OA=5,则A(5,0).根据对称的性质得到:OM=2OB,结合B(4,2)求得M(8,4).然后由待定系数法求一次函数解析式即可.
试题解析:(1)过点B作BD⊥OA于点D,
设BD=a,
∵tan∠AOB=![]() ,
,
∴OD=2BD.
∵∠ODB=90°,OB=2![]() ,
,
∴a2+(2a)2=(2![]() )2,
)2,
解得a=±2(舍去﹣2),
∴a=2.
∴OD=4,
∴B(4,2),
∴k=4×2=8,
∴反比例函数表达式为:y=![]() ;
;
(2)∵tan∠AOB=![]() ,OB=2
,OB=2![]() ,
,
∴AB=![]() OB=
OB=![]() ,
,
∴OA=![]() =
=![]() =5,
=5,
∴A(5,0).
又△AMB与△AOB关于直线AB对称,B(4,2),
∴OM=2OB,
∴M(8,4).
把点M、A的坐标分别代入y=mx+n,得![]() ,
,
解得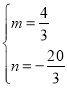 ,
,
故一次函数表达式为:y=![]() x﹣
x﹣![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
